Limit of sinx/x as x approaches infinity, lim x→∞ sinx/x

The limit of sinx/x as x approaches infinity is equal to zero. That is, lim_x→∞ sinx/x = 0. This can be proved using the Squeeze Theorem of limits which will be done here.

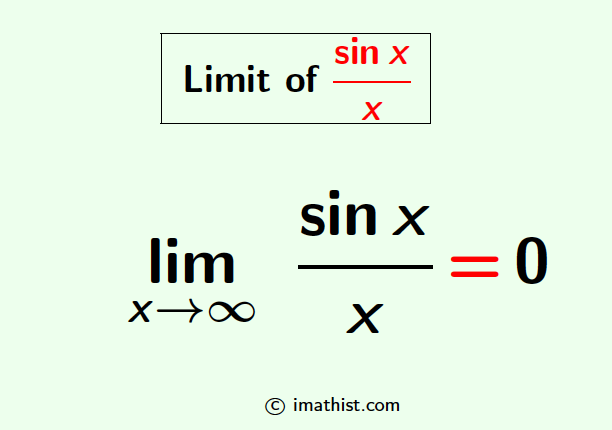
Limit of sinx/x as x goes to infinity

Question: What is the limit of sinx/x when x→∞.

Answer: The limit of sinx/x when x tends to infinity is equal to 0.

Explanation:

We know that the value of sinx lies between -1 and 1 for any real number x, that is,

-1 ≤ sinx ≤ 1

Dividing by x, we get that

$-\dfrac{1}{x} \leq \dfrac{\sin x}{x} \leq \dfrac{1}{x}$

Taking limit x→∞, we obtain that

$-\lim\limits_{x \to \infty} \dfrac{1}{x} \leq \lim\limits_{x \to \infty} \dfrac{\sin x}{x}$ $\leq \lim\limits_{x \to \infty} \dfrac{1}{x}$

⇒ 0 ≤ $\lim\limits_{x \to \infty} \dfrac{\sin x}{x}$ ≤ 0

As $\lim\limits_{x \to \infty} \dfrac{\sin x}{x}$ lies between 0 and 0, it is actually 0. So we obtain that the limit of sinx/x is equal to zero when x goes to infinity. The method used here is known as the Squeeze Theorem of limits.

Read Also: Limit of sinx/x when x→0

Limit of sin(1/x) as x→0 | Limit of cos(1/x) as x→0

Limit of sinx/x when x→∞ | Limit of x/sinx when x→0

Limit of sin(x²)/x when x→0 | Limit of sin(√x)/x when x→0

Remark:

• Following the same approach as above, we can prove that the limit of sinx/x² when x→∞ is also equal to 0.
• As -1 ≤ cosx ≤ 1, by the Squeeze Theorem of limits, we get that the limit of cosx/x when x→∞ is equal to 0.

ALSO READ:

Epsilon-delta definition of limits

Prove that sinx is continuous

Cosx is continuous: proof

Question-Answer

Question 1: Find the limit limx→∞ sin2x/x

Answer:

Note that lim_x→∞ sin2x/x = 2 lim_x→∞ $\dfrac{\sin 2x}{2x}$

Let t=2x. Then t→∞ when x→∞. So we obtain that

lim_x→∞ sin2x/x = 2 lim_t→∞ $\dfrac{\sin t}{t}$ = 2 × 0 (by the above limit)

⇒ lim_x→∞ sin2x/x = 0.

So the limit of sin2x/x as x approaches infinity is equal to 0.

FAQs