The value of the limit of x/sinx as x approaches 0 is equal to 1. In this post, we will learn how to find the limit of $\frac{x}{\sin x}$ when x tends to 0.
lim x/sinx when x approaches 0 Formula
The formula of the limit of x/sinx when x tends to zero is given below:
$\lim\limits_{x \to 0} \dfrac{x}{\sin x}=1$.
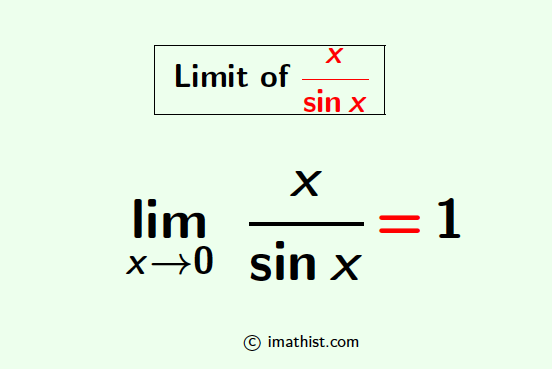
limx→0 x/sinx = 1 Proof
We will use the well-known limit formula for sine functions which is $\lim\limits_{x \to 0} \dfrac{\sin x}{x}=1$ …(I)
Note that
$\lim\limits_{x \to 0} \dfrac{x}{\sin x}$ $=\lim\limits_{x \to 0} \dfrac{1}{\frac{\sin x}{x}}$
= $\dfrac{1}{\lim\limits_{x \to 0} \frac{\sin x}{x}}$
= $\dfrac{1}{1}$ by the above limit formula (I)
= 1.
So the limit of x/sinx when x tends to 0 is equal to 1.
ALSO READ:
| limx→0 (ex-1)/x = 1 | limx→∞ sinx/x = 0 |
| limx→0 (ax-1)/x = lna | limx→0 sinx/x |
| limx→0 sin(1/x) | limx→0 cos(1/x) |
Alternative Proof:
limx→0 x/sinx = 1 can be proved using the L’Hôpital’s rule.
Note that limx→0 x/sinx = 0/sin0 = 0/0, so it is an indeterminate form and we can use L’Hôpital’s rule to find its limit. Now,
$\lim\limits_{x \to 0} \dfrac{x}{\sin x}$
= $\lim\limits_{x \to 0} \dfrac{\frac{d}{dx}(x)}{\frac{d}{dx}(\sin x)}$
= $\lim\limits_{x \to 0} \dfrac{1}{\cos x}$
= $\dfrac{1}{\cos 0}$
= $\dfrac{1}{1}$ as the value of cos0 is 1.
= 1.
So the limit of x/sinx is equal to 1 when x approaches zero, and this is proved by the L’Hôpital’s rule.
More Reading: Solved Problems on Exponential Limits
FAQs
Q1: What is the limit of x/sinx when x approaches 0?
Answer: The limit of x/sinx is equal to 1 when x approaches to 0.