Limit x→0 sinx/x: Formula, Proof | Lim x→0 sinx/x =1 Proof

The limit of sinx/x as x approaches 0, is equal to 1. That is, the limit formula of sinx/x when x→0 is given as follows:

lim_x→0 sinx/x = 1.

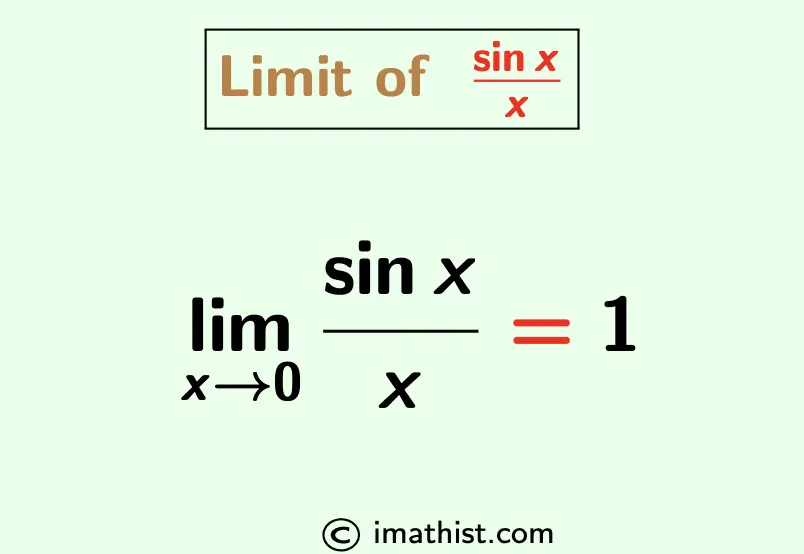
In this post, we will learn how to find the limit of sinx/x when x approaches 0.

Limit of sinx/x as x→0 by l’Hopital’s Rule

Question: What is the limit of sinx/x as x→0?

Answer: lim_x→0 $\dfrac{\sin x}{x}$ = 1.

Explanation:

Note that sin0/0 = 0/0. So the given limit lim_x→0 sinx/x is an indeterminate form and to find its value we will use the l’Hopital’s rule.

By l’Hopital’s rule, we have:

lim_x→0 $\dfrac{\sin x}{x}$

= lim_x→0 $\dfrac{\frac{d}{dx}(\sin x)}{\frac{d}{dx}(x)}$

= lim_x→0 $\dfrac{\cos x}{1}$ as the derivative of sinx is cosx and the derivative of x is 1.

= lim_x→0 $\cos x$

= cos 0

= 1.

Therefore, the limit of sinx/x as x approaches 0 is equal to 1, and this is obtained by the l’Hopital’s rule of limits.

ALSO READ: List of Limit Formulas

Limit of sinx/x when x→∞ | Limit of x/sinx when x→0

Limit of sin(x²)/x when x→0 | Limit of sin(√x)/x when x→0

Limit of sinx/x as x→0 by Squeeze Theorem

Now, we will find the limit of sinx/x by the Sandwich/Squeeze theorem on limits.

It is known that

sin x ≤ x ≤ tan x, for all real x.

⇒ 1 ≤ $\dfrac{x}{\sin x}$ ≤ $\dfrac{\tan x}{\sin x}$

⇒ 1 ≤ $\dfrac{x}{\sin x}$ ≤ $\dfrac{1}{\cos x}$

Letting x→0 on both sides, it follows that

lim_x→0 1 ≤ lim_x→0 $\dfrac{x}{\sin x}$ ≤ lim_x→0 $\dfrac{1}{\cos x}$

⇒ 1 ≤ lim_x→0 $\dfrac{x}{\sin x}$ ≤ 1

So using the squeeze theorem of limits, we get that

lim_x→0 $\dfrac{x}{\sin x}$ = 1

⇒ lim_x→0 $\dfrac{\sin x}{x}$ = 1.

Hence the limit of sinx/x is equal to 1 when x approaches to 0, and this is proved by the Sandwich/Squeeze theorem on limits.

ALSO READ:

Limit of tanx/x when x→∞ | Limit of tanx/x when x→0

Limit of sin(1/x) when x→0 | Limit of cos(1/x) when x→∞

Question: Find the limit lim_x→0 $\dfrac{\sin 3x}{x}$

Solution:

lim_x→0 $\dfrac{\sin 3x}{x}$

lim_x→0 $\dfrac{\sin 3x}{3x} \times 3$

= 3 lim_x→0 $\dfrac{\sin 3x}{3x}$

= 3 lim_z→0 $\dfrac{\sin z}{z}$ where z=3x (so that z→0 when x→0)

= 3 × 1, by the above formula lim_x→0 sinx/x = 1.

= 3

Thus the limit of sin3x/x, when x tends to 0, is equal to 3.

Read These Limit Properties:

Sum rule of limits: Proof | Product rule of limits: Proof

Quotient rule of limits: Proof

FAQs