The limit of sin(1/x) as x approaches 0 does not exist, that is, limx→0 sin(1/x) is undefined. The limit formula of sin(1/x) when x→0 is given below:
limx→0 sin(1/x) = undefined.
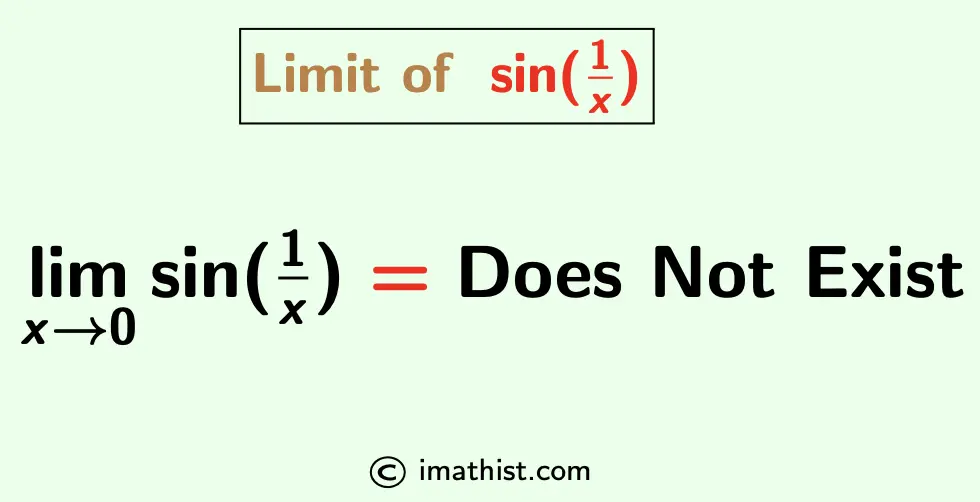
Let us learn how to find the limit of sin(1/x) when x approaches 0.
Find the Limit of sin(1/x) when x→0
Answer: The function sin(1/x) has no defined limit when x→0.
Proof:
We will use the following theorem in order to prove the limit formula limx→0 sin(1/x) = undefined.
Theorem: If limx→c f(x) = L, then for every sequence {xn} converging to c the limit limn→∞ f(xn) always equals to L, that is, the limit will be unique.
Let f(x) = sin(1/x).
To show limx→0 f(x) does not exist, consider two sequences {xn} and {yn}, both converging to 0, but f(xn) and f(yn) converge to different limits. Take
xn = 1/nπ
yn = $\dfrac{1}{(4n+1)\pi/2}$
Note that sin(nπ)=0 and sin (4n+1)π/2 = 1. Also, observe that xn, yn →0 when n tends to ∞. Now we calculate
limn→∞ f(xn) = limn→∞ sin(nπ) = 0.
On the other hand,
limn→∞ f(yn) = limn→∞ sin (4n+1)π/2 = 1.
Thus we deduce that both sequences f(xn) and f(yn) converge to different limits. Hence by the above theorem the limit of sin(1/x) when x→0 does not exist.
ALSO READ:
| limx→0 (ex-1)/x = 1 | limx→∞ sinx/x = 0 |
| limx→0 x/cosx = 0 | limx→0 x/sinx = 1 |
| limx→0 tanx/x = 1 | limx→∞ tanx/x = undefined |
Epsilon – delta definition of limit
FAQs
Q1: What is the limit of sin(1/x) as x approaches 0.
Answer: The limit of sin(1/x) as x approaches 0 is not defined.