Limit of (e^x-1)/x as x approaches 0: Formula, Proof

The limit of (e^x-1)/x, when x tends to zero, is equal to 1. That is, the formula of the lim_x→0 (e^x-1)/x is given by

lim_x→0 (e^x-1)/x = 1.

In this post, we will learn to find the limit of the function (e^x-1)/x when x approaches to zero.

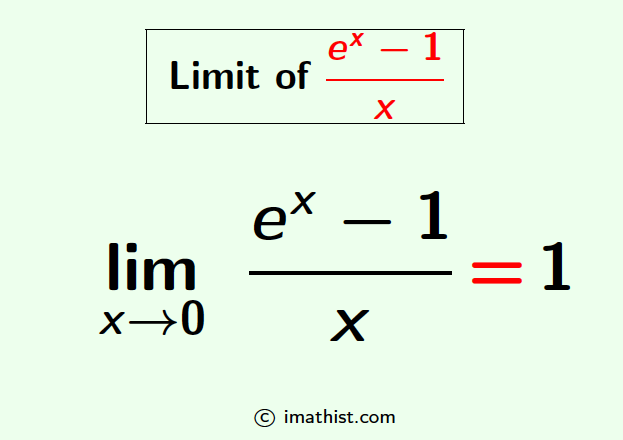
Limit of (e^x-1)/x as x→0

Prove that lim_x→0 $\dfrac{e^x-1}{x}$ = 1.

Proof:

Note that when we put x=0 in the function (e^x-1)/x, we get 0/0, that is, the numerator and denominator both approach 0 as x tends to 0. So the given limit is an indeterminate form.

By l’Hopital’s rule, we have:

lim_x→0 $\dfrac{e^x-1}{x}$

= lim_x→0 $\dfrac{\frac{d}{dx}(e^x-1)}{\frac{d}{dx}(x)}$

= lim_x→0 $\dfrac{\frac{d}{dx}(e^x)-\frac{d}{dx}(1)}{\frac{d}{dx}(x)}$ by the difference rule of derivatives.

= lim_x→0 $\dfrac{e^x-0}{1}$ as the derivative of e^x is e^x and the derivative of xⁿ is nx^n-1 (power rule of derivatives).

= lim_x→0 $e^x$

= e⁰

= 1.

This proves that the limit of (e^x-1)/x, when x goes to 0, is equal to 1. ♣

For the list of all limit formulae, click on the page `List of Limit Formulas`.

ALSO READ:

Limit of (a^x-1)/x when x→0

Limit of (1+$\frac{1}{n}$)ⁿ when n→∞

Limit of sinx/x when x→∞

Limit of x/sinx when x→0

Limit of sin(1/x) when x→0

Question: Evaluate lim_x→0 $\dfrac{e^{2x}-1}{x}$

Solution:

lim_x→0 $\dfrac{e^{2x}-1}{x}$

= lim_x→0 $(\dfrac{e^{2x}-1}{2x} \times 2)$

= 2 lim_x→0 $\dfrac{e^{2x}-1}{2x}$

= 2 lim_t→0 $\dfrac{e^{t}-1}{t}$ where t=2x (so that t→0 when x→0)

= 2 × 1, by the above formula.

= 2

So the limit of (e^2x-1)/x, when x tends to 0, is equal to 2.

You can read: Sum rule of limits: Proof

Product rule of limits: Proof

Quotient rule of limits: Proof

FAQs