Derivative of root sinx by Chain Rule

The derivative of root sinx is equal to cosx/(2√sinx).  In this post, we will learn how to differentiate square root of sinx by the chain rule of derivatives.

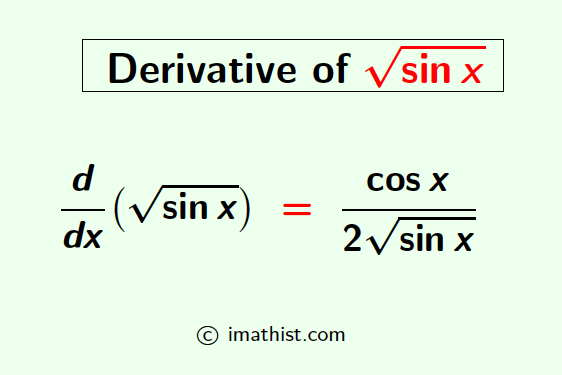
Derivative of Square Root of Sin x by Chain Rule

Question: Find the Derivative of  $\sqrt{\sin x}$ by the chain rule.

Solution:

To find the derivative of root sinx by the chain rule, we will follow the steps provided below.

Step 1: Let z=sinx

Differentiating both sides with respect to x, we get that

$\dfrac{dz}{dx} = \cos x$

Step 2: By the chain rule of derivatives,

$\dfrac{d}{dx}(\sqrt {\sin x})$ = $\dfrac{d}{dx}(\sqrt z)$

= $\dfrac{d}{dz}(\sqrt z) \times \dfrac{dz}{dx}$

= $\dfrac{d}{dz}(z^{1/2}) \times \cos x$ 

= ½ z^{½ -1} × cosx by the power rule of derivatives d/dx(xⁿ)=nx^n-1.

Step 3: Putting z=sinx and simplifying we get that 

$\dfrac{d}{dx}(\sqrt {\sin x})$ = $\dfrac{\cos x}{2 \sqrt{z}}$ as z^-1/2=1/√z.

= $\dfrac{\cos x}{2 \sqrt{\sin x}}$

So the derivative of root sinx is equal to $\dfrac{\cos x}{2 \sqrt{\sin x}}$ and this is obtained by the chain rule of derivatives.

Also Read:

Derivative of $\sqrt{\sin x}$ by First Principle

Derivative of $\sqrt{\cos x}$

Derivative of $\sqrt{e^x}$

FAQs