Simplify 1-cos^2x | 1-cos^2x Formula

The simplification of the expression 1-cos²x is equal to sin²x. In this post, we will learn how to find the formula of 1-cos^2x.

1-cos²x Formula

The formula of 1-cos²x is given below:

1-cos²x = sin²x

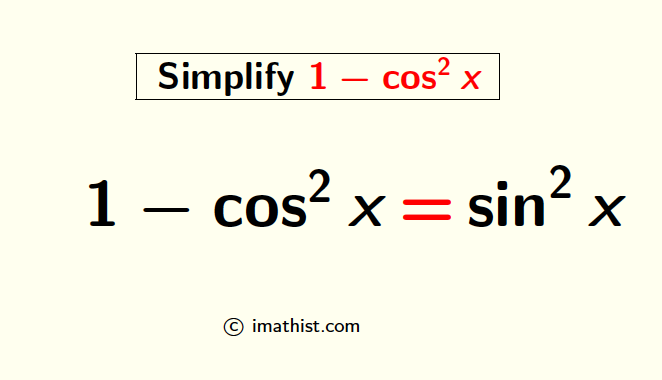
1-cos²x = sin²x Proof

To prove $1-{\cos }^{2}x={\sin }^{2}x$, we will follow the below steps:

Step 1: At first, we will apply the Pythagorean trigonometric identity which is provided below.

${\sin }^{2}x+{\cos }^{2}x=1$  …(I)

Step 2: Next, we will substitute the above value of 1 in the expression $1-{\cos }^{2}x$. This will give us

$1-{\cos }^{2}x=({\sin }^{2}x+{\cos }^{2}x)-{\cos }^{2}x$

$={\sin }^{2}x+{\cos }^{2}x-{\cos }^{2}x$

$={\sin }^{2}x$

So the simplification of $1-{\cos }^{2}x$ is equal to ${\sin }^{2}x$. In other words,

1-cos2x = sin2x

Also Read: Simplify 1-sin²x | Formula of 1+tan²x

Note that if we substitute θ in place of x, we will get the formula of 1-cos²θ which is provided below:

$1-{\cos }^2\theta ={\sin }^2\theta$.

Related Topics:

Simplify cos(x-π)	Values of sin 15, cos 15, tan 15
Simplify sin(π-x)	Values of sin 75, cos 75, tan 75

Question-Answer on 1-cos²x Formula

Question 1: Find the value of $1-{\cos }^2{45}^{\circ }$

Answer:

From the above, we have $1-{\cos }^{2}x={\sin }^{2}x$.

Let us put $x={45}^{\circ }$.

Thus, we get that

$1-{\cos }^2{45}^{\circ }$

$={\sin }^2{45}^{\circ }$

$=({\displaystyle \frac{1}{\sqrt{2}}}{)}^2$

$=1/2$ as we know that $\sin {45}^{\circ }={\displaystyle \frac{1}{\sqrt{2}}}$.

So the value of $1-{\cos }^2{45}^{\circ }$ is equal to $1/2$.

More Trigonometric Identities:

sinx siny Formula | sinx cosy Formula

Formula of cot(x+y)

FAQs