The cot(x+y) formula or the identity is given by
cot(x+y) = $\dfrac{\cot x \cot y -1}{\cot x + \cot y}$.
Here we will prove the formula of cot x+y.
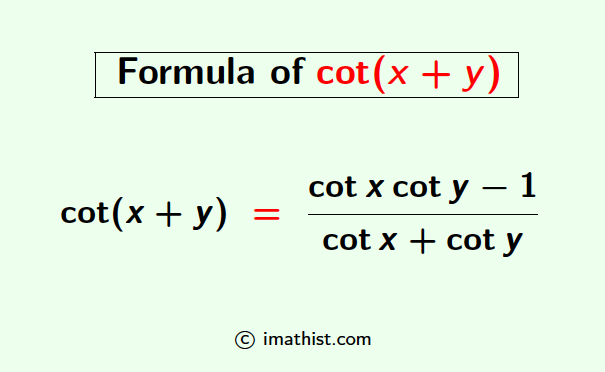
Proof of cot(x+y) Formula
cot(x+y) = $\dfrac{\cot x \cot y -1}{\cot x + \cot y}$.
Proof:
Let us recall the following two formulas:
sin(x+y) = sinx cosy + cosx siny
cos(x+y) = cosx cosy – sinx siny
As $\cot \theta=\frac{\cos \theta}{\sin \theta}$, we have
cot(x+y) = $\dfrac{\cos(x+y)}{\sin(x+y)}$
= $\dfrac{\cos x \cos y – \sin x \sin y}{\sin x \cos y + \cos x \sin y}$
Lets divide both the numerator and the denominator by sinx siny. Thus,
cot(x+y) = $\dfrac{\frac{\cos x \cos y – \sin x \sin y}{\sin x \sin y}}{\frac{\sin x \cos y + \cos x \sin y}{\sin x \sin y}}$
⇒ cot(x+y) = $\dfrac{\frac{\cos x \cos y}{\sin x \sin y} – \frac{\sin x \sin y}{\sin x \sin y}}{\frac{\sin x \cos y}{\sin x \sin y} + \frac{\cos x \sin y}{\sin x \sin y}}$
= $\dfrac{\frac{\cos x}{\sin x } \frac{\cos y}{\sin y}-1}{\frac{\cos x}{\sin x}+ \frac{\cos y}{\sin y}}$
= $\dfrac{\cot x \cot y -1}{\cot x + \cot y}$
Thus the formula of cot(x+y) is equal to cot(x+y) = (cotx coty -1)/(cotx + coty).
cot(x+y) Formula in terms of tan
From the tan(x+y) formula, we know that
tan(x+y) = (tanx + tany)/(1-tanx tany).
Now, since cot is the reciprocal of tan, we get that
cot(x+y) = $\dfrac{1}{\tan (x+y)}$
= $\dfrac{1-\tan x \tan y}{\tan x +\tan y}$.
So the cot(x+y) formula in terms of tan is given below:
cot(x+y) = (1- tanx tany)/(tanx + tany).
Proof of cot(a+b) Formula
cot(a+b) formula or the identity is given by
cot(a+b) = $\dfrac{\cot a \cot b -1}{\cot a + \cot b}$.
Proof:
cot(a+b) = $\dfrac{1}{\tan(a+b)}$
= $\dfrac{1- \tan a \tan b}{\tan a +\tan b}$ as tan(a+b) = (tana + tanb)/(1-tana tanb).
= $\dfrac{1- \frac{1}{\cot a} \frac{1}{\cot b}}{\frac{1}{\cot a} + \frac{1}{\cot b}}$ as tanx=1/cotx.
= $\dfrac{\cot a \cot b -1}{\cot a + \cot b}$
So the cot(a+b) formula is given by cot(a+b) = (cota cotb +1)/(cota + cotb).
ALSO READ:
How to Apply cot(x+y) Formula
Question: Find the value of cot75 degrees.
Solution:
Putting x=45 and y=30 in the above formula of cot(x+y), we will get the value of cot75 degrees.
cot75 = cot(45+30)
= $\dfrac{\cot 45 \cot 30 -1}{\cot 45+ \cot 30}$
= $\dfrac{1 \cdot \sqrt{3} -1}{1+ \sqrt{3}}$
= $\dfrac{\sqrt{3}-1}{\sqrt{3}+1}$
Thus, the value of cot75 degree is equal to (√3-1)/(√3+1) and it is obtained by applying the formula of cot(x+y).
FAQs
Q1: What is the formula of cot(x+y)?
Answer: The formula of cot(x+y) is given by cot(x+y) = (cotx coty-1)/(cotx + coty).
Q2: What is the formula of cot(a+b)?
Answer: The formula of cot(a+b) is equal to cot(a+b) = (cota cotb-1)/(cota +cotb).