Maclaurin series of cosx | Taylor series of cosx

The Maclaurin series expansion of cosx or the Taylor series expansion of cosx at x=0 is given as follows:

cosx = $\sum_{n=0}^\infty \dfrac{(-1)^n}{(2n)!}x^{2n}$

= $1-\dfrac{x^2}{2!}+\dfrac{x^4}{4!}-\dfrac{x^6}{6!}+\cdots$

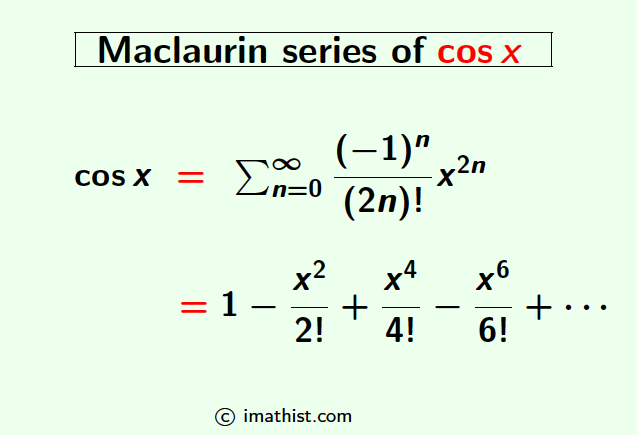
Taylor Series Expansion of Sinx at x=0

Note that the Maclaurin series expansion of f(x)=cosx or the Taylor series of a function f(x) at $x=0$ is given by the following series:

$f(x)=\sum_{n=0}^\infty \dfrac{f^{(n)}(0)}{n!} x^n$ $\cdots (\star)$

So to find the Taylor series of cos(x) at x=0, we put

f(x)=cosx.

We will follow the below steps.

Step 1: We first calculate the n-th derivatives of f(x)=cos x at the point x=0 for every n=0, 1, 2, 3, …, that is, we will find

$[f^{(n)}(x)]_{x=0}$

where $f^{(n)}$ denotes the n-th derivative of f(x). The 0-th derivative of f(x) is the functional value of f(x) at x=0, that is, f(0).

Step 2: As f(x)=cosx, we have

f(0) = cos0 = 1.

Using (sinx)’ = cosx and (cosx)’ = -sinx, we have:

$f'(x)=-\sin x$ ⇒ $f'(0)=-\sin 0=0$

$f^{”}(x)=-\cos x$ ⇒ $f^{”}(0)=-\cos 0=-1$

$f^{(3)}(x)=\sin x$ ⇒ $f^{(3)}(0)=\sin 0=0$

$f^{(4)}(x)=\cos x$ ⇒ $f^{(4)}(0)=\cos 0=1$

$f^{(5)}(x)=-\sin x$ ⇒ $f^{(5)}(0)=-\sin 0=0$

$f^{(6)}(x)=-\cos x$ ⇒ $f^{(6)}(0)=-\cos 0=-1$

$\vdots$

Step 3: Substituting the above values in $(\star)$, the Maclaurin series expansion for f(x)=cosx is equal to

$f(x)=f(0)+xf'(0)+\dfrac{x^2}{2!}f^{”}(0)$ $+\dfrac{x^3}{3!}f^{(3)}(0)$ $+\dfrac{x^4}{4!}f^{(4)}(0)+\dfrac{x^5}{5!}f^{(5)}(0)+\cdots$

⇒ $\cos x$ $=1-\dfrac{x^2}{2!}+\dfrac{x^4}{4!}-\dfrac{x^6}{6!}+\cdots$

Conclusion:  Writing the above series in sigma notation, we obtain the Maclaurin series expansion of cosx which is

$\cos x= \sum_{n=0}^\infty \dfrac{(-1)^n}{(2n)!}x^{2n}$.

Note that the above series for cos x converges for all real values, that is, the radius of converges of cosx series is the interval (-∞, ∞).

Also Read: 

Maclaurin series expansion of sinx

FAQs