tan(x-y) Formula, Proof | tan(x-y) Identity

The tan(x-y) is the tangent of the difference of the angles x and y. Tan(x-y) formula/identity is given as follows:

tan(x-y) = $\dfrac{\tan x -\tan y}{1+\tan x \tan y}$.

In this post, we will prove the formula of tan x-y.

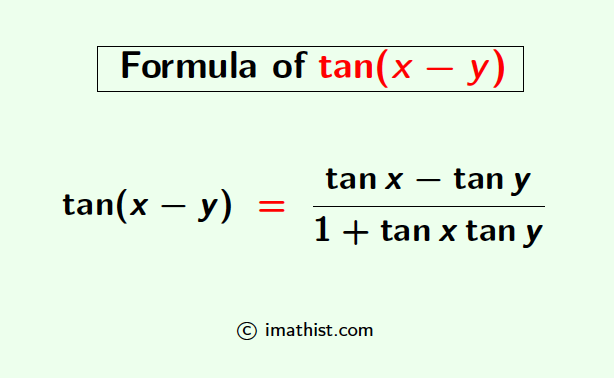
Proof of tan(x-y) Formula

tan(x-y) = $\dfrac{\tan x -\tan y}{1+\tan x \tan y}$

Proof:

We need the below two formulas:

sin(x-y) = sinx cosy – cosx siny

cos(x-y) = sinx siny + cosx cosy

To prove the tan(x-y) formula, we will proceed as follows. Note that $\tan \theta=\frac{\sin \theta}{\cos \theta}$. Thus, we have

tan(x-y) = $\dfrac{\sin(x-y)}{\cos(x-y)}$

⇒ tan(x-y) = $\dfrac{\sin x \cos y – \cos x \sin y}{\sin x \sin y + \cos x \cos y}$

Dividing both the numerator and the denominator by cosx cosy, we obtain that

tan(x-y) = $\dfrac{\frac{\sin x \cos y – \cos x \sin y}{\cos x \cos y}}{\frac{\sin x \sin y + \cos x \cos y}{\cos x \cos y}}$

= $\dfrac{\frac{\sin x \cos y}{\cos x \cos y} – \frac{\cos x \sin y}{\cos x \cos y}}{\frac{\sin x \sin y}{\cos x \cos y} + \frac{\cos x \cos y}{\cos x \cos y}}$

= $\dfrac{\frac{\sin x}{\cos x } – \frac{\sin y}{\cos y}}{\frac{\sin x \sin y}{\cos x \cos y} + 1}$

= $\dfrac{\tan x – \tan y}{1+\tan x \tan y}$

So the formula of tan(x-y) is equal to tan(x-y) = (tanx -tany)/(1+tanx tany).

ALSO READ:

sin(a+b) sin(a-b) Formula

cos(a+b) cos(a-b) Formula

sinx siny Formula

cosx cosy Formula

How to Apply tan(x-y) Formula

Question: Find the value of tan15 degree.

Solution:

To find the value of tan15, one can apply the formula of tan(x-y). Let us put x=45 and y=30 in the formula of tan(x-y) given above. Thus, we have that

tan(45-30) = $\dfrac{\tan 45 -\tan 30}{1+\tan 45 \tan 30}$

= $\dfrac{1 -\frac{1}{\sqrt{3}}}{1+1 \cdot \frac{1}{\sqrt{3}}}$

= $\dfrac{\frac{\sqrt{3}-1}{\sqrt{3}}}{\frac{\sqrt{3}+1}{\sqrt{3}}}$

= $\dfrac{\sqrt{3}-1}{\sqrt{3}+1}$

Thus, the value of tan15 degree is equal to (√3-1)/(√3+1) obtained by applying the formula of tan(x-y).

FAQs