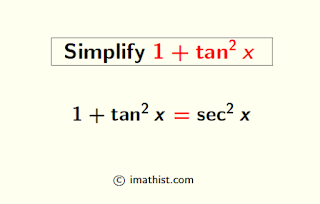The simplification of 1+tan2 x is equal to sec2 x. In this post, we will find the formula of 1+tan2x. This will be proved using trigonometric identities.
1+tan2x Formula
To simplify the expression 1+tan2 x, we will follow the below steps:
Step 1: At first, we put $\tan x=\dfrac{\sin x}{\cos x}$. By doing so, we obtain that
$1+\tan^2 x$ $=1+(\dfrac{\sin x}{\cos x})^2$
$=1+\dfrac{\sin^2 x}{\cos^2 x}$
Step 2: Simplifying the above, we get that
$1+\tan^2 x=1+\dfrac{\sin^2 x}{\cos^2 x}$
$=\dfrac{\sin^2 x+\cos^2 x}{\cos^2 x}$
$=\dfrac{1}{\cos^2 x}$ as we know that $\sin^2 x+\cos^2 x=1$
$=(\dfrac{1}{\cos x})^2$ $=(\sec x)^2$ as the reciprocal of cosx is secx.
$=\sec^2 x$
Conclusion: Thus, the simplification of $1+\tan^2 x$ is equal to $\sec^2 x$.
Note that we also have that $1+\tan^2 \theta=\sec^2 \theta$ obtained in a similar way as above.
Also Read:
sinx=0, cosx=0, tanx=0 General Solution
Values of sin 15, cos 15, tan 15
Values of sin 75, cos 75, tan 75
Question-Answer on 1+tan2x Formula
Question 1: Find the value of 1+tan2 $45^\circ$
Answer:
From the above, we get that the value of 1+tan2 x is equal to sec2 x. In this formula, we put $x=45^\circ$. Thus, we have
$1+\tan^2 45^\circ$ $=\sec^2 45^\circ$
$=\dfrac{1}{\cos^2 45^\circ}$
$=\dfrac{1}{(\dfrac{1}{\sqrt{2}})^2}$ as we know that $\cos 45^\circ =\dfrac{1}{\sqrt{2}}$.
$=\dfrac{1}{1/2}=2$
Thus, the value of $1+\tan^2 45^\circ$ is equal to $2$.
FAQs
Q1: What is the formula of 1+tan2x?
Answer: The formula of 1+tan2x is given as follows: 1+tan2x = sec2x.