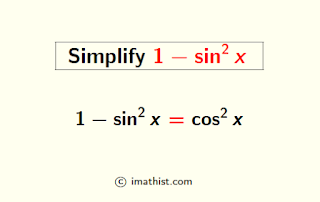Simplify the Expression 1-sin^2x | 1-sin^2x Formula, Identity

The value of the expression 1-sin^2(x) is equal to cos^2(x). In this post, we will find the formula of 1-sin^2x.

1-sin²x Formula

To simplify the expression 1 – sin²x, we will follow the below steps:

Step 1: Let us apply the following Pythagorean trigonometric identity:

1 = sin²x + cos²x 

Step 2: Now, we substitute the above value of 1 in the expression 1 – sin²x. By doing so we get that

1 – sin²x = (sin²x + cos²x) – sin²x

= sin²x + cos²x – sin²x

= cos² x

Thus, the formula of 1-sin²x is equal to cos²x .

Note that we also have that $1-\sin^2 \theta=\cos^2 \theta$ and this is obtained in a similar way as above.

Also Read:

sinx=0, cosx=0, tanx=0 General Solution

Formula of 1+tan^2 x

Simplify cos(x-pi)

Values of sin 15, cos 15, tan 15

Values of sin 75, cos 75, tan 75

Question-Answer on 1-sin2x Formula

Question 1: Find the value of $1-\sin^2 60^\circ$

Answer:

From the above, we get the value of $1-\sin^2 x$ which is equal to $\cos^2 x$. In this formula, we put $x=60^\circ$. So we get that

$1-\sin^2 60^\circ$

$=\cos^2 60^\circ$

$=(\dfrac{1}{2})^2$

$=1/4$ as we know that $\cos 60^\circ =1/2$.

Thus, the value of $1-\sin^2 60^\circ$ is equal to $1/4$.

FAQs