sin(pi-x) Formula | Formula of sin(pi-theta)

 For any x, sin(pi-x) formula is given below:

sin(pi-x)=sinx

Similarly, sin(pi-theta)=sin theta. In this post, we will learn how to compute sin(pi-x) or sin(pi-theta).

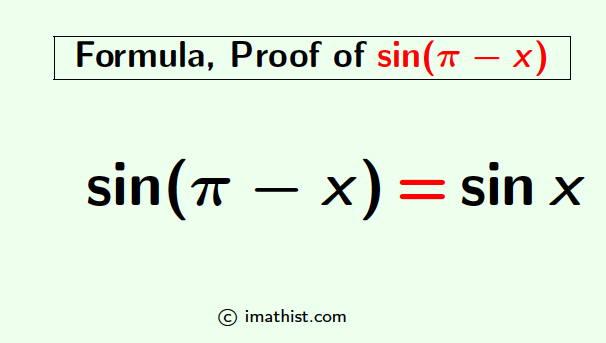
sin(pi-x) Simplify

To find the formula of sin(π-x), we will apply the following trigonometric identity:

sin(A-B) = sinA cosB – cosA sinB …(∗)

Here we put A=π and B=x; so that we get

sin(π-x) = sinπ cosx – cosπ sinx

= 0⋅cosx – (-1) sinx as we know that sinπ=0 and cosπ=-1.

= sinx.

Thus we have established the formula of sin(π-x) which is given by

sin(π-x) = sinx

Note: In a similar way, we obtain the formula of sin(π-θ) which is given by sin(π-θ) = sinθ.

More Readings: How to Simplify cos(π-x)

Values of sin15, cos 15, tan15

General Solution of tanx=tany

General Solution of sinx=1 | General Solution of sinx=-1

Simplify sin(x-pi)

The formula of sin(x-π) is given by

sin(x-π) = -sinx.

To prove it, we will put A=x, B=π in (*). Thus, we obtain that

sin(x-π) = sinx cosπ – cosx sinπ

= sinx⋅ (-1) – cosx ⋅ 0

= -sinx.

Hence, we obtain the formula of sin(x-π) which is equal to sin(x-π) = -sinx.

Also Read:

How to simplify cos(sin-1x)

1-sec2x Formula

1+cot2x Formula

FAQs