General Solutions of sinx=-1 | Solve sinx=-1

The general solutions of sinx=-1 are given by x=(4n-1)π/2 where n is any integer. In this post, we will learn how to find the general solutions of the trigonometric equation sinx=-1.

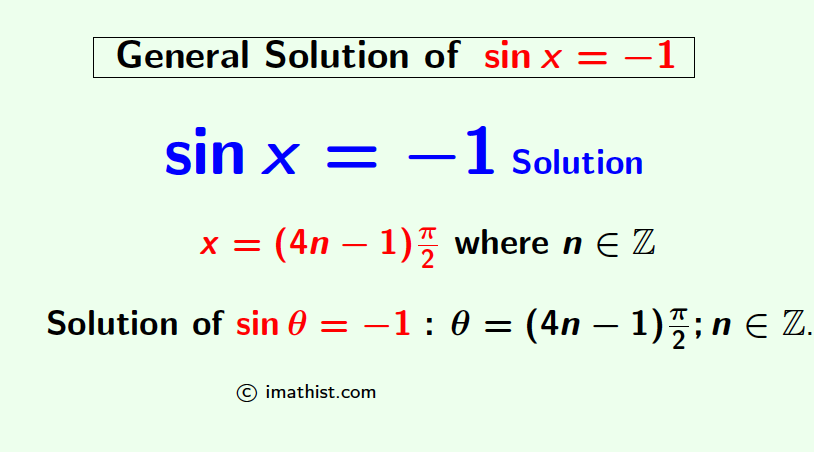
sinx=-1 General Solution

Question: Find the general solutions of sinx= -1.

Answer:

As sin(-π/2)= -1, the equation sinx= -1 can be written

sinx = sin(-π/2).

∴ x=mπ+(-1)^m $(-\frac{\pi}{2})$ for some integers m. [Since the general solutions of sinθ = sinα are given by θ = nπ+(-1)ⁿ α, n ∈ Z.]

Case 1: First assume that m is even, that is, m=2n where n is an integer. So

x=2nπ+(-1)²ⁿ $(-\frac{\pi}{2})$

= 2nπ-$\frac{\pi}{2}$

= (4n-1)$\frac{\pi}{2}$ …(I) 

Case 2: Next, assume that m is odd, that is, m=2n+1 for some integer n. So

x=(2n+1)π+(-1)²ⁿ⁺¹ $(-\frac{\pi}{2})$

= (2n+1)π+$\frac{\pi}{2}$

= 2nπ+$\frac{3\pi}{2}$

= (4n+3)$\frac{\pi}{2}$ …(II)

Combining (I) and (II), we deduce that x=(4n-1)π/2.

So the general solution of sinx=1 equals x=(4n-1)π/2 where n is any integer. As n can be any integer, so sinx=-1 has infinite solutions.

Let us now find the general solutions of sin2x=-1 as an application of the general solution of sinx=-1.

sin2x=-1 General Solution

Question: Find the general solutions of sin2x= -1.

Answer:

From the above, we know that the general solutions of sinθ=-1 are given by θ=(4n-1)π/2 where n ∈ Z.

So the general solutions of sin2x=-1 are equal to

2x = (4n-1)π/2 where n ∈ Z.

⇒ x = (4n-1)π/4.

So the general solutions of sin2x= -1 are given by x=(4n-1)π/4 where n is an integer.

ALSO READ:

tanx=tany General Solution	x=nπ+y; n ∈ Z
sinx=0 General Solution	x=nπ; n ∈ Z
sinx=1 General Solution	x=(4n+1)π/2; n ∈ Z

FAQs