Simplify 1+cot^2x | 1+cot^2x Formula [in terms of cosec]

The simplification or the formula of 1+cot²x is given as follows:

1+cot²x = cosec²x.

In this post, we will learn how to establish the formula of 1+cot²x.

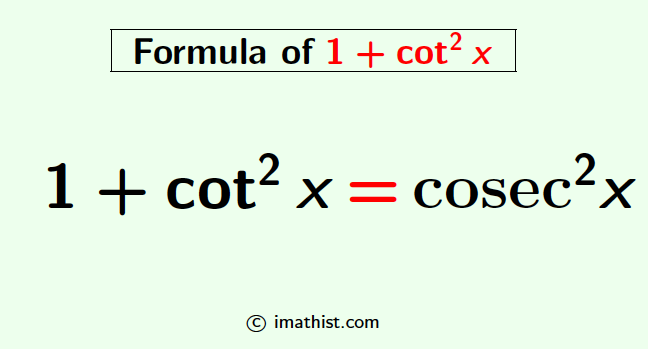
Proof of 1+cot²x Formula

Question: Prove the formula 1+cot²x = cosec²x.

Solution:

L.H.S. = 1+cot²x

= $1+(\dfrac{\cos x}{\sin x})^2$ as cotx=cosx/sinx.

= $1+\dfrac{\cos^2 x}{\sin^2 x}$

= $\dfrac{\sin^2 x + \cos^2 x}{\sin^2 x}$

= $\dfrac{1}{\sin^2 x}$ as we know that sin²x+cos²x=1.

= $(\dfrac{1}{\sin x})^2$

= cosec²x [∵ cosecx = 1/sinx]

= R.H.S.

So we have proven the formula of 1+cot²x in terms of cosec which is given by 1+cot²x = cosec²x.

Question-Answer

Question: Find the value of 1+cot²45.

Answer:

In the above formula of 1+cot²x = cosec²x, we put x=45 degrees. So we get that

1+cot²45 = cosec²45 = (√2)² = 2.

So the value of 1+cot²45 is equal to 2.

ALSO READ:

Simplify 1-cos²x

1+tan²x Formula

Simplify cos⁴x+sin⁴x

cot(x+y) Formula, Proof

tan(x-y) Formula, Proof

FAQs