dy/dx=y/x Solve the Differential Equation

The general solution of the differential equation dy/dx=y/x is given by y=cx where c is any constant. We will use the separation of variables method.

Let us learn how to find the solution of dy/dx=y/x.

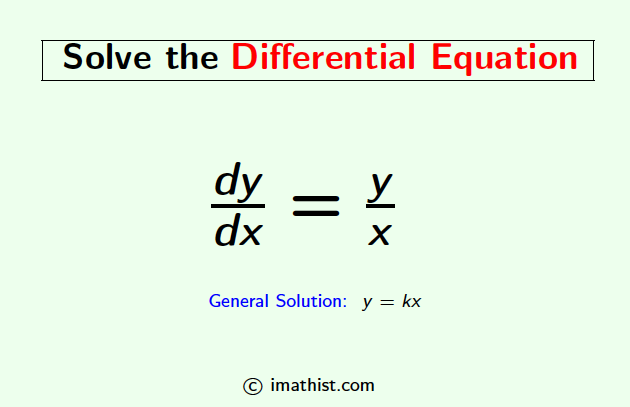
General Solution of dy/dx=y/x

Question: Find the general solution of $\dfrac{dy}{dx}=\dfrac{y}{x}$.

Answer:

$\dfrac{dy}{dx}=\dfrac{y}{x}$

We can rewrite it as

$\dfrac{dy}{y}=\dfrac{dx}{x}$

Integrating both sides, we get that

$\int \dfrac{dy}{y}=\int \dfrac{dx}{x} +C$ where C is a constant of integration.

⇒ ln|y| = ln|x| + ln|c| where ln is the natural logarithm, that is, ln=log_e and we replace C with another constant ln|c|

⇒ ln|y| = ln|cx| by the logarithm rules

⇒ y=cx

So the general solution of dy/dx=y/x is equal to y=cx where c is any constant. This is obtained by the separation of variables method.

More Reading: Solve $\dfrac{dy}{dx}=\dfrac{x}{y}$

Solve dy/dx = sin(x+y) | Solve dy/dx = cos(x+y)

Solve dy/dx = e^(x+y)

Particular Solution of dy/dx=y/x

Question: Find the particular solution of $\dfrac{dy}{dx}=\dfrac{y}{x}, y(1)=1$.

Answer:

We know that y=cx is the general solution of dy/dx=y/x.

Given y(1)=1, that is, x=1, y=1.

So from y=cx we have

1=c ⋅ 1

⇒ c=1.

So y=x is the particular solution of dy/dx=y/x when y(1)=1.

FAQs