Solve dy/dx=cos(x+y) and Find General Solution

The general solution of the differential equation dy/dx=cos(x+y) is equal to tan(x+y)/2 = x+C. Here we learn how to solve dy/dx=cos(x+y).

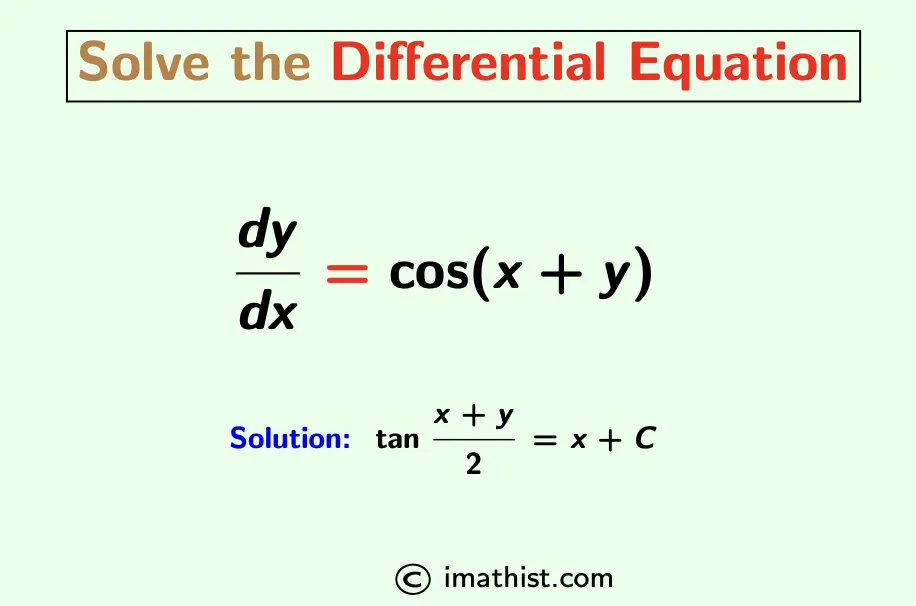
Find General Solution of dy/dx=cos(x+y)

Question: What is the solution of dy/dx=cos(x+y)?

Answer: The solution of dy/dx=cos(x+y) is tan(x+y)/2 = x+C.

Solution:

Let x+y=2u

So 1+ $\dfrac{dy}{dx}$ = 2 $\dfrac{du}{dx}$

⇒ $\dfrac{dy}{dx}$ = 2 $\dfrac{du}{dx}$ -1.

Thus, the given equation dy/dx=cos(x+y) becomes

2 $\dfrac{du}{dx}$ -1 = cos 2u

⇒ 2 $\dfrac{du}{dx}$ = 1+ cos 2u

⇒ 2 $\dfrac{du}{dx}$ = 2cos²u, by the formula 1+ cos 2x = 2cos²x

⇒ $\dfrac{du}{dx}$ = cos²u

⇒ sec²u du = dx

Integrating, ∫sec²u du = ∫dx +C

⇒ tan u = x+C

⇒ tan $\dfrac{x+y}{2}$ = x+C as 2u=x+y.

So the solution of dy/dx=cos(x+y) is tan $\dfrac{x+y}{2}$ = x+C where C is a constant.

ALSO READ:

Solve dy/dx=y/x	Solve dy/dx = x/y
Solve dy/dx=sin(x+y)	Solve dy/dx=ex+y

Alternative Method:

Let z=x+y.

Differentiating with respect to x, we get that

$\dfrac{dz}{dx}=1+\dfrac{dy}{dx}$

⇒ $\dfrac{dy}{dx}=\dfrac{dz}{dx}-1$

Substituting the above values in the given differential equation dy/dx = cos(x+y), we obtain that

$\dfrac{dz}{dx}$ -1 = cos z

⇒ dz/dx = 1+cos z

Rewriting, $\dfrac{dz}{1+\cos z}=dx$

Thus, ∫ $\dfrac{dz}{1+\cos z}$ = ∫dx +C

Multiplying the numerator and the denominator by 1-cos z, we have that

∫ $\dfrac{1-\cos z}{(1+\cos z)(1-\cos z)} dz$ = ∫dx +C

⇒ ∫ $\dfrac{1-\cos z}{1-\cos^2 z} dz$ = ∫dx +C

⇒ ∫ $\dfrac{1-\cos z}{\sin^2 z} dz$ = ∫dx +C [using the formula cos²z +sin²z=1]

⇒ ∫ $\dfrac{1}{\sin^2 z} dz$ – ∫ $\dfrac{\cos z}{\sin^2 z} dz$ = ∫dx +C

⇒ ∫ cosec²z dz – ∫cosecz cotz dz = ∫dx +C

⇒ – cot z + cosec z = x +C as the integral of cosec²x is -cotx and the integral of cosecs cote is -cosecx.

⇒ -cot(x+y) + cosec(x+y) = x +C as z=x+y.

So the solution of dy/dx=cos(x+y) is equal to cosec(x+y) -cot(x+y)= x +C where C is an integral constant.

FAQs