How to Integrate sin^3x cos^2x | Integration of sin^3x cos^2x

The integration of sin^3x cos^2x is equal to (cos⁵x)/5 – (cos³x)/3 +C where C is a constant. Here we learn how to integrate sin^3x cos^2x.

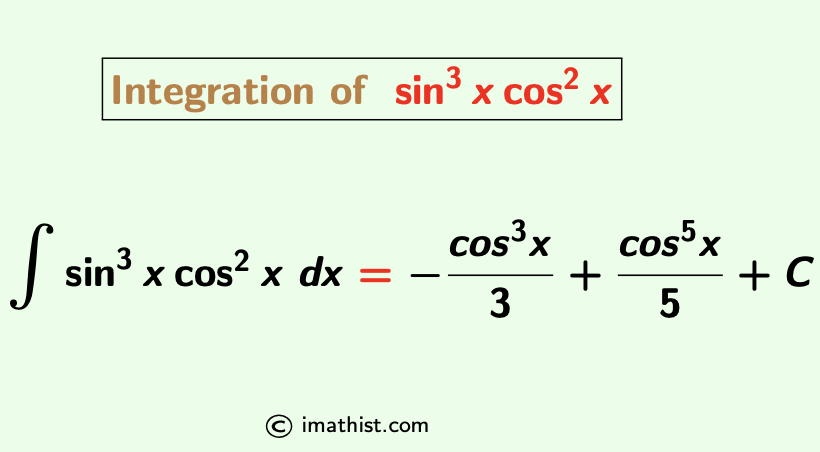
What is the Integration of sin³x cos²x?

Question: Find the integral of sin³x cos²x, that is,

Find ∫sin³x cos²x dx

Solution:

We have:

∫sin³x cos²x dx = ∫sin²x sin x cos²x dx

⇒ ∫sin³x cos²x dx = ∫(1 -cos²x) cos²x sin x dx [by the formula sin²x = 1 -cos²x]

Put cosx =z, so that -sinx dx =dz.

∴ From above, we have that

∫sin³x cos²x dx = – ∫(1 – z²) z² dz

= – ∫(z² – z⁴) dz

= – ∫z² dz + ∫z⁴ dz

= – z³/3 + z⁵/5 +C

= – cos³x/3 + cos⁵x/5 +C

So the integration of sin³x cos²x equals to – cos³x/3 + cos⁵x/5 +C, that is, the integral of sin cube x cos square x is given by the formula:

∫sin3x cos2x dx = – cos3x/3 + cos5x/5 +C

Related Integrals:

Integration of sinx cosx dx

Integration of sin²x dx

Integration of cos²x dx

Integral of sin³x dx

FAQs