dy/dx=x/y Solve the Differential Equation [General Solution]

The general solution of the differential equation dy/dx=x/y is given by y² = x² + C where C is an integral constant. Here we will learn how to find the solution of dy/dx=x/y.

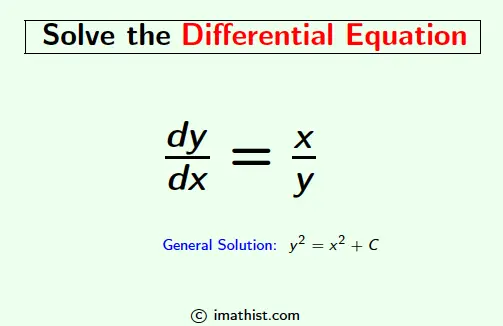
General Solution of dy/dx=x/y

Question: Find the general solution of dy/dx=x/y.

Answer:

The given differential equation is

$\dfrac{dy}{dx}=\dfrac{x}{y}$

Separating the variables x and y, we get that

y dy = x dx

Integrating both sides, we get that

∫y dy = ∫x dx +C’ where C’ is a constant of integration.

⇒ y²/2 = x²/2 + C/2 where C’=C/2

⇒ y² = x² + C

So the general solution of dy/dx=x/y is equal to y² = x² + C where C is an arbitrary constant.

ALSO READ:

Solve dy/dx=y/x

Particular Solution of dy/dx=x/y

Question: Find the particular solution of dy/dx = x/y, y(0)=0.

Answer:

From above, the solution of dy/dx=x/y is equal to y² = x² + C.

Given that y(0)=0, so y=0 when x=0.

Thus from y² = x² + C we get that

0² = 0² + C

⇒ C=0.

So the particular solution of dy/dx=x/y when y(0)=0 is equal to y² = x², that is y=±√x.

FAQs