Derivative of 1/x: Proof by First Principle

The derivative of 1/x is equal to -1/x². In this blog post, we will learn how to find the differentiation of 1/x.

Derivative of 1/x Formula: The formula of the derivative of 1/x is given by

d/dx(1/x) = -1/x².

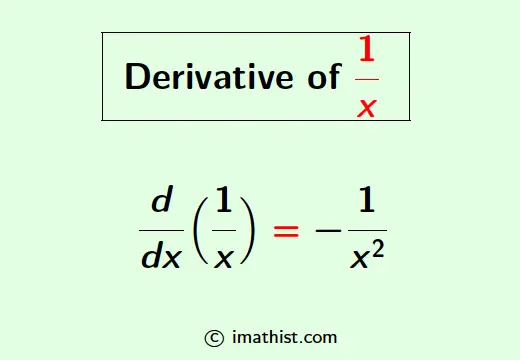
Let us find the differentiation of 1/x by first principle which is equal to -1/x².

Derivative of 1/x using First Principle

By the first principle, the derivative of a function f(x) is given by the following limit formula:

$\dfrac{d}{dx}(f(x))$ = lim_h→0 $\dfrac{f(x+h)-f(x)}{h}$

Let f(x) = 1/x in the above limit. So the derivative of 1/x from the first principle will be equal to

∴ $\dfrac{d}{dx}(1/x)$ $=\lim\limits_{h \to 0} \dfrac{\dfrac{1}{x+h}-\dfrac{1}{x}}{h}$

= lim_h→0 $\dfrac{x-(x+h)}{hx(x+h)}$

= lim_h→0 $\dfrac{x-x-h}{hx(x+h)}$

= lim_h→0 $\dfrac{-h}{x(x+h)}$

= $\dfrac{-1}{x(x+0)}$

= $-\dfrac{1}{x\cdot x}$

= -1/x²

Thus, the derivative of 1/x is equal to -1/x² and this is obtained by the first principle of derivatives.

Also Read:

Derivative of 1/√x	Derivative of (√x + 1/√x)
Derivative of x √x	Derivative of 1/x2

What is the Derivative of 1/x?

The derivative of 1/x can be obtained by using the power rule of derivatives. Recall, the power rule of derivatives:

$\dfrac{d}{dx}(x^n)$ = nx^n-1

First, write $1/x$ as follows:

$\dfrac{1}{x} = x^{-1}$

Differentiate both sides with respect to x. So we obtain that

$\dfrac{d}{dx}(\dfrac{1}{x}) = \dfrac{d}{dx}(x^{-1})$ = -1 × x^-1-1 = -1/x².

So the derivative of 1/x by the power of derivatives is equal to -1/x².

Derivative of |x|	Derivative of 1/2x
Derivative of √x	Derivative of 2x

Question Answer

Question: What is d/dx(1/x) at x=1?

Answer:

From above, we know that d/dx(1/x) = -1/x². So at the point x=1, the value of the differentiation of 1/x will be equal to

[d/dx(1/x)]_x=1 = -1/1² = -1.

So the derivative of 1/x at x=1 is equal to -1.

FAQs