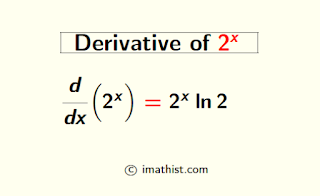[Solved] What is the Derivative of 2^x [2 to the x]?

The derivative of 2^x is equal to 2^x ln2. Here, ln denotes the natural logarithm (logarithm with base e). In this post, we will find the derivative of 2 to the power x.

Derivative of 2^x Formula

As we know that the derivative of a^x is a^xln a, the formula for the derivative of 2^x will be as follows:

$\dfrac{d}{dx}(2^x)=2^x \ln 2$

or

$(2^x)’=2^x \ln 2$.

Here, the prime $’$ denotes the first-order derivative.

What is the Derivative of 2^x?

Answer: The derivative of 2^x is 2^xln 2.

Explanation:

We will use the logarithmic differentiation to find the derivative of 2 raised to x. To do so, let us put

z=2^x

Taking natural logarithms $\ln$ of both sides, we obtain that

$\ln z=\ln 2^x$

$\Rightarrow \ln z=x\ln 2$ as we know that ln a^b = b ln a

Differentiating both sides with respect to x, we get that

$\dfrac{1}{z} \dfrac{dz}{dx}=\ln 2$

$\Rightarrow \dfrac{dz}{dx}=z\ln 2$

$\Rightarrow \dfrac{dz}{dx}=2^x\ln 2$ as z=2^x.

Thus, the derivative of 2^x is 2^x ln2.

Also Read: 

Derivative of e²

Derivative of Pi

Derivative of sin4x

Derivative of sin5x

Derivative of 2^x at x=0

From the above, we obtain the derivative of 2^x which is equal to 2^x ln 2. So the derivative of 2 to the power x at x=0 will be equal to

$d/dx[2^x]{x=0}$ $=[2^x \ln 2]{x=0}$

= 2⁰ ln 2

= ln 2 as we know that x⁰=1 for any non-zeero x.

Thus, the derivative of  2^x at x=0 is ln 2.

Also Read:

Derivative of sin⁵ x

Derivative of cos(e^x

FAQs