Derivative of mod x | Mod x Derivative

Derivative of absolute value of x. The derivative of mod x is denoted by d/dx(|x|) and it is equal to x/|x| for all nonzero values of x. In this post, we will learn how to differentiate modulus x.

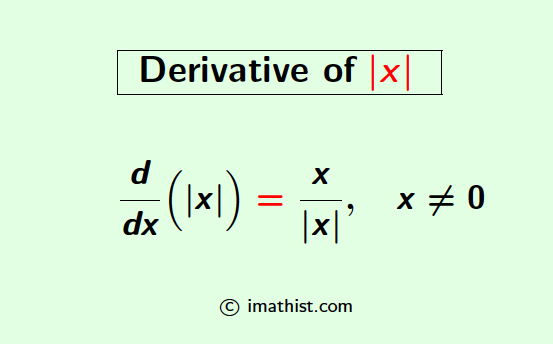
Recall that mod x is defined as below.

$|x|=\begin{cases} x, & \text{ if } x\geq 0 \\ -x, & \text{ if } x< 0 \end{cases}$

Derivative of |x|

The derivative of |x|, that is, the derivative of modulus x, denoted by d/dx(|x|), is given as follows:

$\dfrac{d}{dx}(|x|)=\dfrac{x}{|x|}$ for $x \neq 0$.

How to Differentiate mod x?

Let us now find the derivative of mod x.

Question: Find $\dfrac{d}{dx}(|x|)$.

Answer:

Case 1: First we assume that x>0.

Thus, by the above definition of |x|, we have |x|=x.

∴ d/dx(|x|) = d/dx(x) = 1

Case 2: First we assume that x<0.

So, again by the above definition of |x|, we have |x|=-x.

In this case, d/dx(|x|) = d/dx(-x) = -1

Thus, we obtain that

$\dfrac{d}{dx}(|x|)=\begin{cases} 1, & \text{ if } x> 0 \\ -1, & \text{ if } x< 0 \end{cases}$

Combining both cases, we get that

$\dfrac{d}{dx}(|x|)=\dfrac{x}{|x|}$ for $x \neq 0$.

NOTE: The function f(x)=|x| is not differentiable. For a proof, CLICK HERE.

More Derivatives: Derivative of mod sinx

Derivative of mod cosx

Remark:

1. The derivative of mod x at x=a>0 is 1.
2. The derivative of mod x at x=a<0 is -1.
3. The derivative of mod x at x=0 does not exist.

ALSO READ:

Derivative of 2^x

Derivative of 10^x

Derivative of x^x

FAQs