Derivative of mod sinx | Mod sinx Derivative

The derivative of the modulus of sinx is equal to (sinx cosx)/|sinx|. In this post, we will learn how to differentiate mod sinx, that is, how to find d/dx(|sinx|).

• The derivative of mod sin x is denoted by d/dx(|sinx|).
• d/dx(|sinx|) = (sinx cosx)/|sinx|, when sinx is non-zero.

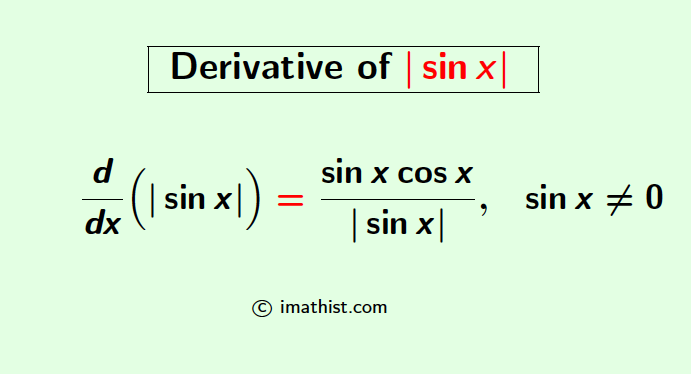
The differentiation formula of mod sinx is given below and we will learn how to derive this formula in details.

Mod sinx Derivative Formula

The derivative of mod sinx is as follows:

$\dfrac{d}{dx}(|\sin x|)=\dfrac{\sin x \cos x}{|\sin x|}$,

provided that sinx is non-zero. Before proving this formula, let us recall the derivative of mod x which is given below:

$\dfrac{d}{dx}(|x|)=\dfrac{x}{|x|}$ for $x \neq 0$ …(I)

Derivative of modulus of sinx

Question: Find $\dfrac{d}{dx}(|\sin x|)$.

Answer:

We will use the cahin rule of derivatives and the above formula (I) to find the derivative of mod sinx. Let us put

z=sinx.

⇒ dz/dx = cosx …(II)

Then by the chain rule,

$\dfrac{d}{dx}(|\sin x|)$ = $\dfrac{d}{dz}(|z|) \times \dfrac{dz}{dx}$

= $\dfrac{z}{|z|} \times \cos x$ by (I) and (II)

= $\dfrac{\sin x \cos x}{|\sin x|}$ as z=sinx.

So the derivative of mod sinx is (sinx cosx)/|sinx| and this is obtained by the chain rule of derivatives.

Question-Answer

Question 1: Find the derivative of mod sin2x.

Answer:

Let us put t=2x.

So dt/dx = 2

Now, by the chain rule of derivatives,

$\dfrac{d}{dx}(|\sin 2x|)$ = $\dfrac{d}{dt}(|\sin t|) \times \dfrac{dt}{dx}$

= $\dfrac{\sin t \cos t}{|\sin t|} \times 2$ by the above formula.

= $\dfrac{2\sin t \cos t}{|\sin t|}$

= $\dfrac{\sin 2t}{|\sin t|}$ using the formula sin2x=2sinx cosx.

= $\dfrac{\sin 4x}{|\sin 2x|}$ as t=2x.

So the derivative of mod sin2x is equal to sin4x/|sin2x|.

ALSO READ:

Derivative of mod x	Derivative of root x
Derivative of root sinx	Derivative of root ex

FAQs