The general solution of the differential equation dy/dx=sin(x+y) is given by tan(x+y) – sec(x+y) = x +C where C is an arbitrary constant. Here we will learn how to find the solution of dy/dx=sin(x+y).
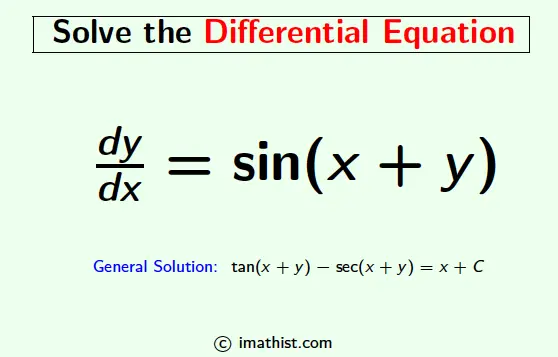
Let us now solve the differential equation dy/dx=sin(x+y) by the substitution method.
General Solution of dy/dx=sin(x+y)
Question: Find the general solution of dy/dx=sin(x+y).
Answer:
Step 1: Use the substitution z=x+y.
Differentiating w.r.t x, we get
$\dfrac{dz}{dx}=1+\dfrac{dy}{dx}$
⇒ $\dfrac{dy}{dx}=\dfrac{dz}{dx}-1$
Step 2: Use the above data in the given differential equation which is dy/dx=sin(x+y). Thus, we deduce that
$\dfrac{dz}{dx}$ -1 = sin z
⇒ dz/dx = 1+sinz
Step 3: Separate the variables x and z and rewrite the above equation. Therefore,
$\dfrac{dz}{1+\sin z}=dx$
Step 4: Integrating both sides of the above equation,
∫ $\dfrac{dz}{1+\sin z}$ = ∫dx +C
Integrating both sides, we get that
⇒ ∫ $\dfrac{1-\sin z}{(1+\sin z)(1-\sin z)} dz$ = ∫dx +C
⇒ ∫ $\dfrac{1-\sin z}{1-\sin^2 z} dz$ = ∫dx +C
⇒ ∫ $\dfrac{1-\sin z}{\cos^2 z} dz$ = ∫dx +C
⇒ ∫ sec2z dz – ∫secz tanz dz = ∫dx +C
⇒ tan z – sec z = x +C
⇒ tan(x+y) – sec(x+y) = x +C
So the general solution of dy/dx=sin(x+y) is equal to tan(x+y) – sec(x+y) = x +C where C is an integral constant.
ALSO READ:
FAQs
Q: What is the general solution of dy/dx=sin(x+y)?
Answer: The general solution of dy/dx=sin(x+y) is tan(x+y) – sec(x+y) = x +C where C is any constant.