Limit of log(1+x)/x as x approaches 0

The limit of log(1+x)/x as x approaches 0 is equal to 1. The lim_{x -> 0} (log(1 + x))/x formula is given by

$\lim\limits_{x \to 0} \dfrac{\log(1+x)}{x}=1$.

In this post, we will learn to prove the limit of log(1+x)/x when x tends to zero.

Table of Contents

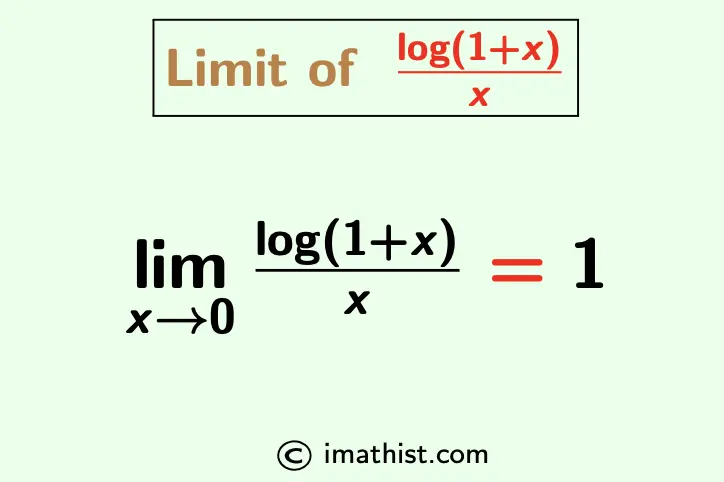
Lim_{x → 0} log(1 + x)/x

Prove that lim_{x → 0} log(1 + x)/x = 1.

Answer:

Note that the given limit can be written as

$\lim\limits_{x \to 0} \dfrac{1}{x} \log(1+x)$

= $\lim\limits_{x \to 0} \log(1+x)^{\frac{1}{x}}$ by the logarithm rules

= $\log \lim\limits_{x \to 0} (1+x)^{\frac{1}{x}}$ using the property lim_x→0 log(f(x)) = log lim_x→0 f(x).

= $\log e$ by the limit formula lim_x→0 (1+x)^1/x = e.

= 1 if the base is e.

So the limit of log(1+x)/x is equal to 1 when x→0, provided that the logarithm base is e.

More Limits:

Answer: The limit of log(1+x)/x when x tends to 0 is equal to 1, that is, lim_x→0 log(1 + x)/x =1.

Spread the love