Integral of 1/x^n (1 by x power n): Formula, Proof

The integral of 1/x^n (1 by x power n) is equal to x^-n+1/(1-n) +C. Here we will learn how to integrate 1/xⁿ using the power rule of integration.

The integration formula of 1/xⁿ is given by

$\int \dfrac{dx}{x^n}=\dfrac{x^{1-n}}{1-n}+C$

where C denotes an integral constant.

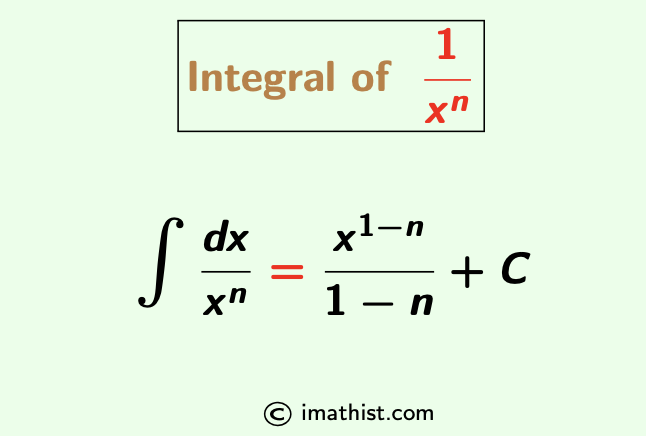
Integration of 1/xⁿ

The integral of 1/xⁿ is denoted by ∫dx/xⁿ. We have:

$\int \dfrac{dx}{x^n}$

= $\int x^{-n} \, dx$ by the rule of indices.

= $\dfrac{x^{-n+1}}{1-n}+C$ by the power rule of integrations.

So the integration of 1 by x^n is equal to x^1-n/(1-n) +C (C is a constant), and this is obtained by the power rule of integrals.

You Can Read These Integrals:

Integral of ln(x) | Integral of sin²x

Integral of cos²x | Integral of sin³x

Definite Integral of 1/xⁿ

Question: Find the integration of 1/xⁿ from 0 to 1, that is,

Find $\int_0^1 \dfrac{dx}{x^n}$.

Answer:

AS the integration of 1/xⁿ is equal to x^-n+1/(1-n) +C by above, we obtain that

$\int_0^1 \dfrac{dx}{x^n}$

= $\Big[\dfrac{x^{1-n}}{1-n} \Big]_0^1$

= $\dfrac{1^{1-n}}{1-n} – \dfrac{0^{1-n}}{1-n}$

= $\dfrac{1}{1-n} – 0$

= $\dfrac{1}{1-n}$.

So the integration of 1/xⁿ from 0 to 1 is equal to 1/(n-1).

More Reading: How to integrate 2^x

Integration of square root of a²+x²

Integration of square root of a²-x²

FAQs