Integral of lnx: Formula, Proof

The integral of lnx is equal to ∫ln(x)= xln x -x+C where C is an integral constant. Here we will learn how to integrate lnx, that is, find ∫ln(x).

The integral formula of lnx is given below:

∫ln(x) dx = xln(x) -x+C where ln(x) = logex.

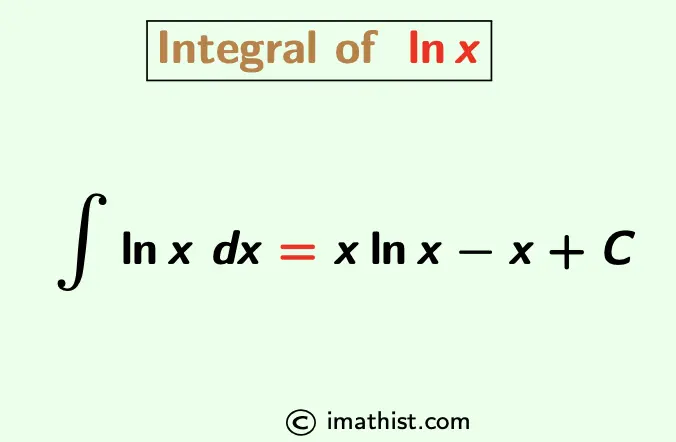
Integration of lnx

To find the integration of lnx, we will use the integration by parts formula. The formula is given below.

∫uv dx = u∫v dx -∫[$\frac{du}{dx}$∫v dx] dx.

Put u=lnx and v=1.

Therefore,

∫ln(x) dx

= $\displaystyle \int \ln x \cdot 1 \ dx$

= $\ln x \displaystyle \int 1\ dx – \displaystyle \int \left[\dfrac{d}{dx}(\ln x) \int 1\ dx \right]dx$

= $\ln x \times x -\displaystyle \int \left[\dfrac{1}{x} \times x \right]dx$ + C

= $x\ln x -\int dx + C$

= $x\ln x -x+C$, where C is an integration constant.

So the integral of lnx is equal to ∫ln(x)= xlnx-x+C and this is derived using the integration by parts formula.

Have You Read These Integrals?

Integration of √tanx

Integration of lnx

Integration of 2^x

Integration of tan²x

Question-Answers

Question: Find integral of lnx from 1 to 2.

That is, find $\displaystyle \int_1^2 \ln x \ dx$.

Answer:

From above, we have $\int \ln x \ dx = x\ln x -x$. So we obtain that

$\displaystyle\int_1^2 \ln x \ dx = \left[x\ln x -x \right]_1^2$

= (2ln2 – 2) -(ln1 – 1)

= 2ln2 -2 +1 as ln1=0

= 2ln2 – 1.

Thus, the integration of lnx from 1 to 2 is equal to 2ln2 – 1.

ALSO READ:

Integration of cube root x

Integration of square root x

FAQs on Integration of lnx