Laplace Transform of t^2 | Laplace of t square

The Laplace transform of t square is equal to 2/s³. In this post, we will learn about the formula of L{t²} along with its proof.

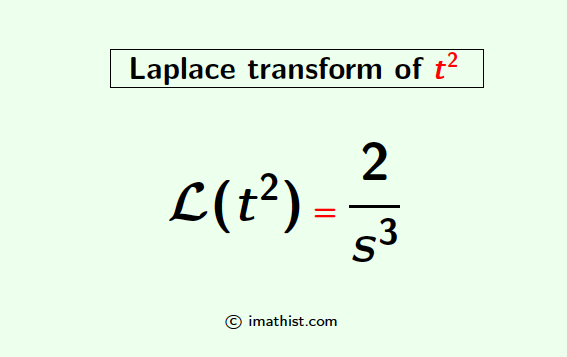
Laplace Transform of t² Formula

The Laplace of t square formula is given as follows

L{t²} = 2/s³.

Laplace Transform of t² Proof

We will now prove that the Laplace transform of t² is L{t²} = 2/s³. By the definition of Laplace ransforms, we have

L{f(t)} = $\int_0^\infty e^{-st} f(t) dt$

So, L{t²} = $\int_0^\infty t^2 e^{-st} dt$ …(I)

Put x=st

∴ dx=s dt

⇒ dt = dx/s. Note that t=x/s.

t	x
0	0
∞	∞

So from (I), the Laplace of t² will be equal to

L{t²} = $\int_0^\infty (\dfrac{x}{s})^2 e^{-x} \dfrac{dx}{s}$

= $\dfrac{1}{s^3}$ $\int_0^\infty x^2 e^{-x} dx$

= $\dfrac{1}{s^3} \Gamma(3)$ where the Gamma function is defined as follows: $\Gamma(z)=\int_0^\infty x^{z-1} e^{-x} dx$

= $\dfrac{1}{s^3} \times 2$ as we know that $\Gamma(n)=(n-1)!$

= $\dfrac{2}{s^3}$

So the Laplace transform of t square by the definition is equal to 2/s³.

More Laplace Transforms:

Laplace transform of 2

Laplace transform of t²

Laplace transform of sint

FAQs