Integral of e^2x | e^2x Integration

The integration of e^2x is equal to e^2x/2. In this post, we will learn how to integrate e to the 2x. The integration of e^2x can be derived directly from the formula of the integral of e^mx which is given below:

∫e^mx dx = $\dfrac{e^{mx}}{m}$ +C where C is an integration constant.

Putting m=2 in the above formula, the integral of e to the 2x is equal to

∫e^2x dx = $\dfrac{e^{2x}}{2}$ +C.

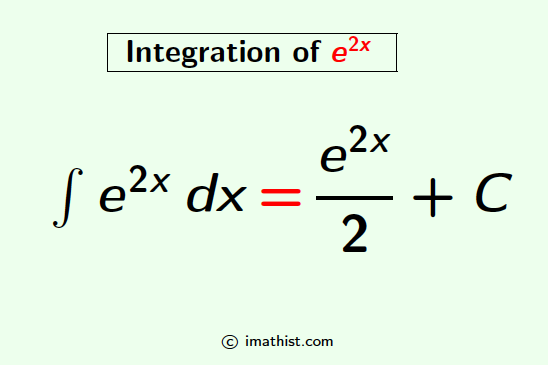
What is the Integration of e^2x

Question: What is the integration of e^2x?

Answer: The integration of e^2x is $\dfrac{e^{2x}}{2}$+C.

Explanation:

We will find the integration of e^2x by the substitution method, we will follow the below steps.

Step 1: Let us put $t=2x$.

Differentiating both sides with respect to x, we have

$\dfrac{dt}{dx}=2$

⇒ $dx= \dfrac{dt}{2}$

Step 2: Let us now put the values of 2x and dx in the original integration. By doing so, we will get that

∴ ∫e^2x dx = ∫ $e^t \dfrac{dt}{2}$

= $\dfrac{1}{2}$ ∫ e^t dt as 1/2 is a constant, so we can take it out of the integration.

= $\dfrac{1}{2}$ e^t +C as the integration of e^x is e^x

= $\dfrac{1}{2}$ e^2x + C as t=2x.

So the integration of e^2xdx is $\dfrac{1}{2}$ e^2x +C where C is an integral constant.

Verification: To verify the integration of e^2x is e^2x/2 +C, we need to show that the derivative of e^2x/2 +C is equal to e^2x.

Now, d/dx (e^2x/2 +C)

= d/dx(e^2x/2) + d/dx(C)

= 2e^2x/2 + 0 as the derivative of a constant is zero and d/dx (e^ax) = ae^ax.

= e^2x.

So the integration of e^2x is equal to e^2x/2 +C is verified.

More Integrals: Integral of e^3x

Integration of tan x | Integration of cot x

Integration of secx | Integration of cosecx

Definite Integral of e^2x

Question: Find the definite integral $\int_0^1 e^{2x} dx$.

Answer:

We have shown above that the integration of $e^{2x} dx$ is $\dfrac{1}{2} e^{2x}$. Thus, we have that

$\int_0^1 e^{2x} dx$

$=[\dfrac{1}{2} e^{2x}]_0^1$

$=\dfrac{1}{2}[e^{2x}]_0^1$

$=\dfrac{1}{2}(e^{2 \cdot 1} -e^0)$

$=\dfrac{1}{2}(e^2 -1)$

So the definite integration of e^2x from 0 to 1 is equal to (e²-1)/2.

Also Read: 

Derivative of x^3/2

Derivative of $\sqrt{x}+\dfrac{1}{\sqrt{x}}$

Derivative of 1/logx

Derivative of e^1/x

FAQs