Derivative of x^1/x (x to the power 1/x)

The derivative of x^1/x (x to the power 1/x) is denoted by d/dx(x^1/x) and its value is equal to x^1/x[1/x² – 1/x² ⋅ log_ex].

The derivative formula of x^1/x is given below:

d/dx(x^1/x) = x^{1/x -2} [1 – log_ex].

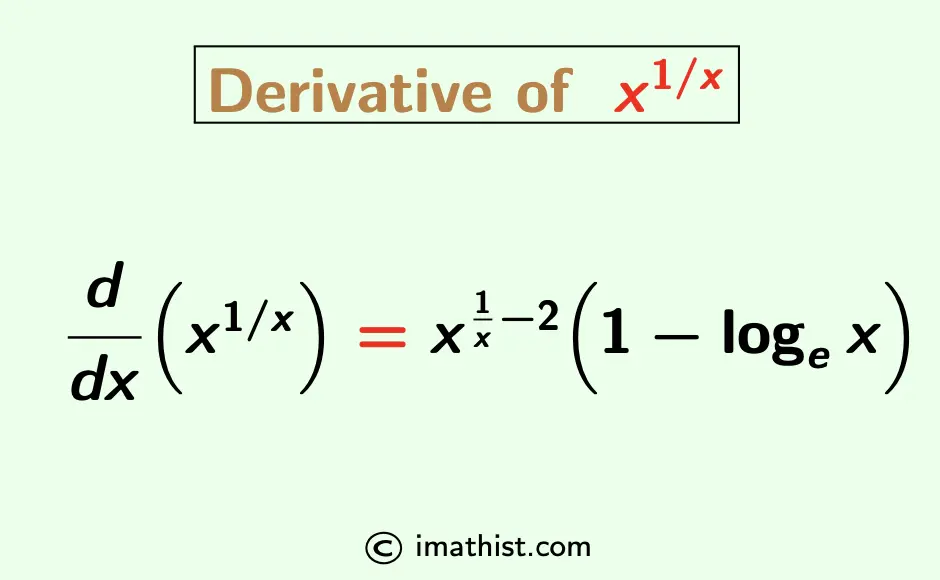
Let us now learn how to differentiate x^1/x.

Derivative of x to the power 1/x

Question: Prove that d/dx(x1/x) = x1/x -2 [1 – logex].

Answer:

Let us put

y=x^1/x.

Here we need to find dy/dx. Taking logarithms on both sides, we get that

log_e y = log_e x^1/x

⇒ log_ey = 1/x ⋅ log_ex, as we know the logarithm formula log_abⁿ = n log_ab.

Differentiating both sides w.r.t x, we have

$\dfrac{d}{dx}(\log_e y)=\dfrac{d}{dx}(\dfrac{1}{x} \log_e x)$

⇒ $\dfrac{1}{y} \dfrac{dy}{dx}$ $=\dfrac{1}{x} \dfrac{d}{dx}(\log_e x)+\log_e x\dfrac{d}{dx}(\dfrac{1}{x})$, by the product rule of derivatives.

⇒ $\dfrac{1}{y} \dfrac{dy}{dx}$ $=\dfrac{1}{x} \cdot \dfrac{1}{x}+\log_e x \cdot \dfrac{-1}{x^2}$ as we know d/dx(log_ex) =1/x and the derivative of 1/x is equal to -1/x².

⇒ $\dfrac{dy}{dx}=y(\dfrac{1}{x^2}-\dfrac{1}{x^2\log_e x}$

= $x^{\frac{1}{x}} \dfrac{1}{x^2} \Big(1-\log_e x \Big)$ as y=x^1/x.

= x^{1/x -2} [1 – log_ex].

So the derivative of x^1/x (x to the power 1/x) is equal to x^{1/x -2} [1 – log_ex], and it is obtained by the logarithmic differentiation.

More Derivatives:

Derivative of x^x | Derivative of x^sinx

Find the derivative of x^tanx

Derivative of x^cosx

Derivative of sinx/x | Derivative of x^logx

FAQs