Derivative of sinx/x | sinx/x Derivative

The derivative of sinx/x is equal to (xcosx -sinx)/x². Here we will learn how to differentiate sinx/x with respect to x.

The derivative formula of sinx/x is given by

$\dfrac{d}{dx}(\dfrac{\sin x}{x})$ = $\dfrac{x\cos x -\sin x}{x^2}$.

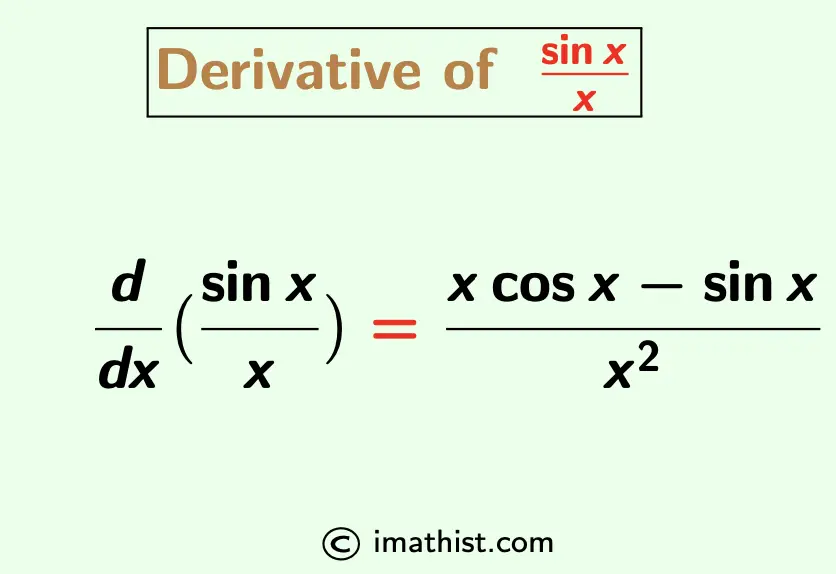
Find the Derivative of sinx/x

As sinx/x is a quotient function, to find the derivative of sinx/x we will use the quotient rule of derivatives. By the rule, the derivative of $\dfrac{f}{g}$ is given by

$\big(\dfrac{f}{g}\big)’$ = $\dfrac{gf’-fg’}{g^2}$

where $’$ denotes the first order derivative with respect to x.

Put f=sinx and g=x, the derivative of sinx/x is equal to

$\big(\dfrac{\sin x}{x}\big)’$ = $\dfrac{x \cdot (\sin x)’-\sin x \cdot (x)’}{x^2}$

= $\dfrac{x \cdot \cos x-\sin x \cdot 1}{x^2}$ as the derivative of sinx is cosx and the derivative of x is 1.

= $\dfrac{x \cdot \cos x-\sin x \cdot 1}{x^2}$

= $\dfrac{x\cos x -\sin x}{x^2}$.

So the derivative of sinx/x is (xcosx -sinx)/x² and it is obtained by the quotient rule of derivatives.

ALSO READ:

Derivative of xsinx	Derivative of 1/sinx
Derivative of x sinx	Derivative of sinx cosx

Question-Answer on Derivative of sinx/x

Question: What is the derivative of sinx/x at x=1?

Answer:

From above, the derivative of sinx/x at x=1 is equal to

[(sinx/x)$’$] = [(xcosx -sinx)/x²]_x=1

= (1 ⋅ cos1 -sin1)/1²

= cos1 -sin1.

So the derivative of sinx/x at the point x=1 is equal to cos1 -sin1.

Have You Read These Derivatives?

Derivative of 1/x	Derivative of √sinx
Derivative of 1/ln x	Derivative of √cosx

FAQs