Derivative of 1/lnx | How to Differentiate 1/lnx

The derivative of 1/lnx is equal to -1/x(lnx)². In this post, we will learn how to differentiate 1 divided by lnx with respect to x.

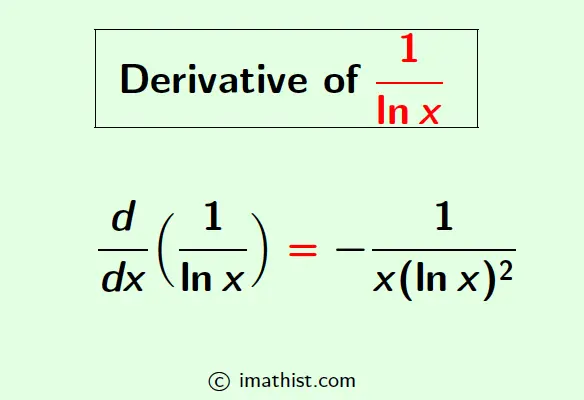
Let us now find the derivative of 1/lnx using the chain rule and the power rule of derivatives.

What is the Derivative of 1/lnx?

Answer: The derivative of 1/lnx with respect to x is equal to -1/x(lnx)². So the derivative formula of 1/lnx is given by

$\dfrac{d}{dx}(\dfrac{1}{\ln x})$ = $-\dfrac{1}{x(\ln x)^2}$.

Solution:

Let us put t=lnx.

Differentiating, dt/dx = 1/x.

Now, by the chain rule of derivatives, the derivative of 1 divided by lnx is equal to

$\dfrac{d}{dx}(\dfrac{1}{\ln x})$

= $\dfrac{d}{dt}(\dfrac{1}{t}) \times \dfrac{dt}{dx}$

= $\dfrac{d}{dt}(t^{-1}) \times \dfrac{1}{x}$

= -1 × t^-1-1 × 1/x as we know that d/dt(tⁿ)=nt^n-1.

= -1/xt²

= -1/x(lnx)² , putting back the value of t=lnx.

Hence the derivative of 1/lnx is equal to -1/x(lnx)² and this is obtained by the chain rule and power rule of derivatives.

Derivative of 1/lnx by Quotient Rule

Proof:

As 1/lnx is a quotient function, the derivative of 1/lnx can be evaluated by the quotient rule of derivatives. The quotient rule of derivatives is given below:

$\dfrac{d}{dx} \left(\dfrac{f}{g} \right)$ = $\dfrac{g \frac{df}{dx} – f \frac{dg}{dx}}{g^2}$

Put f=1 and g=lnx. So by the above quotient rule,

$\dfrac{d}{dx}(\dfrac{1}{\ln x})$

= $\dfrac{\ln x \frac{d}{dx}(1) – 1 \frac{d}{dx}(\ln x)}{(\ln x)^2}$

= $\dfrac{\ln x \cdot 0 – 1 \cdot \frac{1}{x}}{(\ln x)^2}$ as the derivative of a constant is zero and the derivative of lnx is 1/x.

= $\dfrac{-\frac{1}{x}}{(\ln x)^2}$

= $- \dfrac{1}{x(\ln x)^2}$

So the derivative of 1/lnx is -1/x(lnx)², obtained by the quotient rule of derivatives.

ALSO READ:

Derivative of 1/sinx: The derivative of 1/sinx is -cosecx cotx.

Derivative of xx: The derivative of xx is xx(1+lnx).

Derivative of 1/cosx: The derivative of 1/cosx is secx tanx.

Derivative of 1/logx: The derivative of 1/logx is -1/x(log x)2.

FAQs