Derivative of Square Root of 2x | Root 2x Derivative

The derivative of square root of 2x is equal to 1/√(2x). In this post, we will learn how to find the derivative of the square root of 2x.

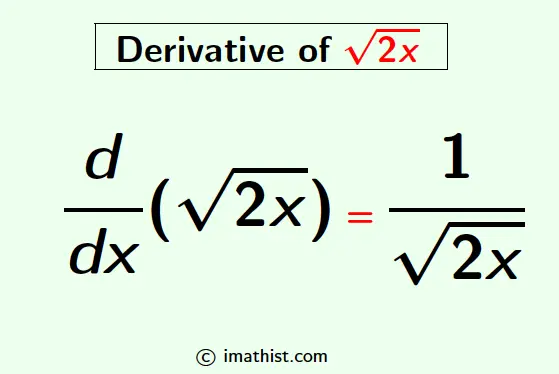
The derivative of the square root of 2x is given by the following formula:

$\dfrac{d}{dx}(\sqrt{2x})$ = $\dfrac{1}{\sqrt{2x}}$

Derivative of root 2x by Power Rule

To find the derivative of the square root of 2x, we will use the power rule of derivatives. The power rule is used to find the derivative of xⁿ which is given by the formula:

$\frac{d}{dx}$(xⁿ) = nx^n-1.

Note that $\sqrt{2x}$ =√2 x^1/2. Thus,

$\dfrac{d}{dx}(\sqrt{2x})$ = $\dfrac{d}{dx}$(√2 x^1/2)

= √2 × $\dfrac{d}{dx}$(x^1/2), by the constant rule of derivatives.

= $\sqrt{2} \times \dfrac{1}{2}$ x^{1/2 – 1} by the above power rule.

= $\dfrac{\sqrt{2}}{2}$ x^-1/2

= $\dfrac{1}{\sqrt{2x}}$.

So the derivative of root 2x is equal to 1/√(2x), and this is obtained by the power rule of derivatives.

Next, let us find the derivative of the square root of 2x by the chain rule of derivatives.

Derivative of root 2x by Chain Rule

Let t=2x.

So dt/dx =2.

By the chain rule, the derivative of root 2x

= $\dfrac{d}{dx}(\sqrt{2x})$

= $\dfrac{d}{dt}$(√t) × dt/dx

= $\dfrac{1}{2\sqrt{t}}$ × dt/dx as the derivative of root x is 1/(2√x).

= $\dfrac{1}{2\sqrt{2x}}$ × 2 as t=2x.

= 1/√(2x)

So the derivative of square root 2x is equal to 1/√(2x), and this is obtained by the chain rule of derivatives.

Have You Read These?

Derivative of 1/2x

Derivative of root 3x

Derivative of root x

FAQs