Formula of cos^2x-sin^2x | cos^2x-sin^2x Formula, Identity

The formula of cos^2x – sin^2x is equal to cos2x. Let us learn how to establish the proof the identity of cos²x-sin²x.

cos²x-sin²x formula is given by cos²x-sin²x = cos2x.

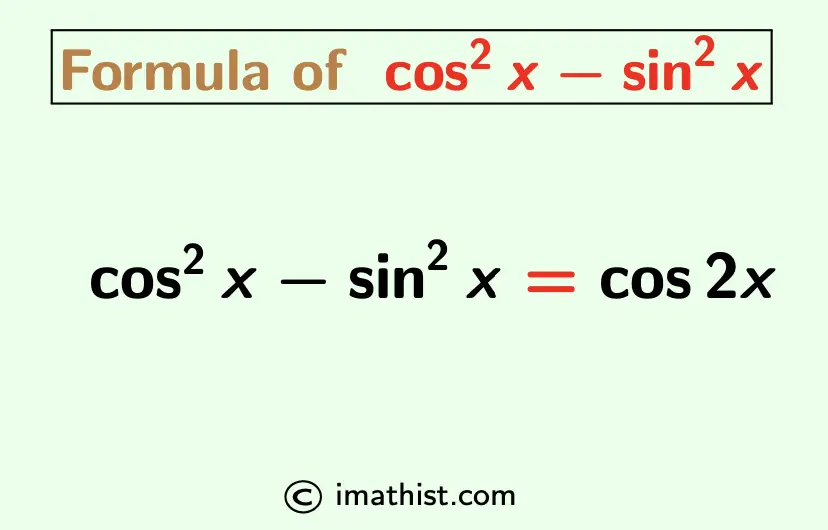
Proof of cos²x-sin²x Formula

Question: Prove that cos²x-sin²x = cos2x.

Proof:

cos²x-sin²x

= cosx ⋅ cosx – sinx ⋅ sinx

= cos(x+x), here we have used the identity cosa cosb – sina sinb = cos(a+b).

= cos 2x

So cos^2x – sin^2x is equal to cos2x and we have proved this cos²x-sin²x formula by using the identity of cos(a+b).

Question-Answer

Question 1: Find the value of cos²45° -sin²45°.

Answer:

Putting x=45° in the above formula cos²x-sin²x = cos2x, we obtain that

cos²45° -sin²45°

= cos (2×45)°

= cos90°

= 0 as the value of cos90° is 0.

Thus the value of cos²45° -sin²45° is equal to 0.

Related Topics:

1-cos2x Formula	Solutions of sinx=1
sin(pi/2-x) Formula	1+cot2x Formula

FAQs