Sin(90-theta) Formula, Proof | Simplify Sin(θ-90)

The sin(90-theta) formula is given by sin(90-θ) = cosθ. As 90°=π/2, sin(90-θ) formula can be written as follows:

sin(π/2-θ) = cosθ.

On the other hand, sin(θ-90) formula is given by sin(θ-90) = -cosθ.

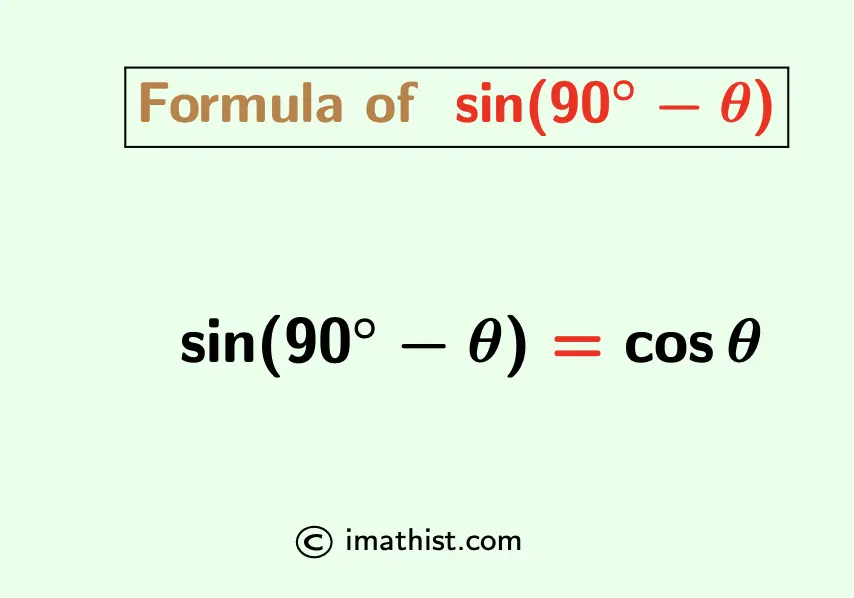
Let us now simplify the expression sin(90-theta).

Simplify Sin(90-theta)

Question: Simplify the expression sin(90-θ).

Answer:

To simplify the expression sin(90-θ), we will use the following formulas:

1. sin(a-b) = sina cosb – cosa sinb.
2. sin90 = 1.
3. cos90 =0.

Let us put a=90 and b=θ in the above formula of sin(a-b). So we obtain that

sin(90-θ) = sin90 cosθ – cos90 sinθ

= 1⋅cosθ – 0⋅sinθ

= cosθ – 0

= cosθ.

So value of sin(90-θ) is equal to cosθ.

sin(90-θ) = cosθ

Also Read: Find the value of sin(5π/2)

sin3x formula in terms of sinx

How to simplify cos(sin^-1x)

Simplify Sin(θ-90)

Question: How to simplify Sin(θ-90)?

Solution:

Note that

Sin(θ-90) = sinθ cos90 – cosθ sin90

= sinθ × 0 – cosθ × 1

= 0 – cosθ

= – cosθ.

So the simplification of sin(θ-90) is equal to -cosθ, that is the value of sin(θ-90) = -cosθ.

sin(θ-90) = -cosθ

Read Also: Simplify sin(π-x)

How to simplify sin(cos^-1x)

FAQs