The formula of cosh2x-sinh2x is given by cosh2x-sinh2x =1. Here we will learn how to prove cosh^2x-sinh^2x=1.
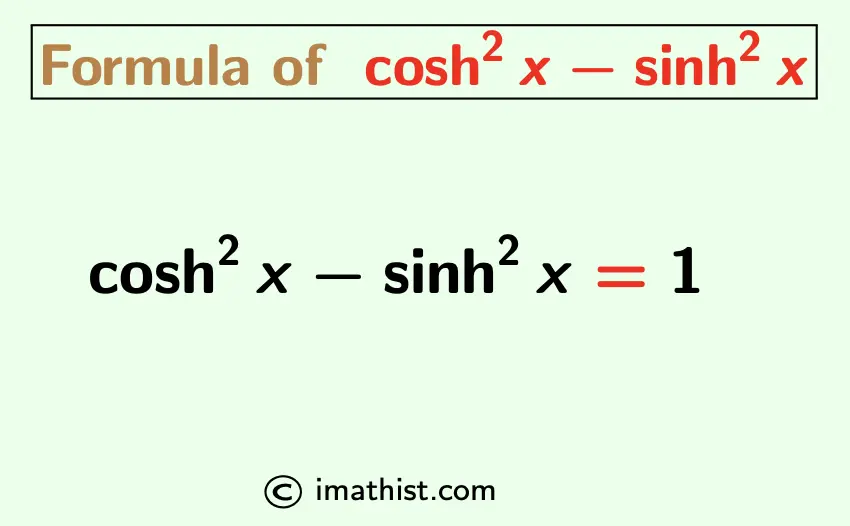
Before we prove the identity cosh2x-sinh2x=1, let us recall that
- coshx = (ex +e-x)/2
- sinhx = (ex – e-x)/2.
Proof of cosh^2x-sinh^2x=1
Question: Prove that cosh2x-sinh2x =1.
Answer:
By the above two formulas, we have that
L.H.S = cosh2x – sinh2x
= $\Big(\dfrac{e^x+e^{-x}}{2} \Big)^2$ $- \Big(\dfrac{e^x-e^{-x}}{2} \Big)^2$
= $\Big(\dfrac{e^x}{2}+\dfrac{e^{-x}}{2} \Big)^2$ $- \Big(\dfrac{e^x}{2}-\dfrac{e^{-x}}{2} \Big)^2$
= 4 × $\dfrac{e^x}{2}$ × $\dfrac{e^{-x}}{2}$ using the formula (a+b)2 – (a-b)2 =4ab.
= ex × e-x
= ex-x
= e0
= 1 = R.H.S.
Hence, we have the proved the identity cosh2x-sinh2x =1.
Related Formulas:
FAQs
Q1: What is the formula of cosh^2x-sinh^2x?
Answer: The formula/identity of cosh^2x-sinh^2x is given by cosh2x-sinh2x =1.