Derivative of coshx: Formula, Proof | coshx Derivative

The derivative of coshx, denoted by d/dx(coshx), is equal to sinhx. Here we will learn how to differentiate cosh(x), i.e, how to find the derivative of the hyperbolic cosine function with respect to x.

The formula of the derivative of coshx is given below:

d/dx[coshx] = sinhx.

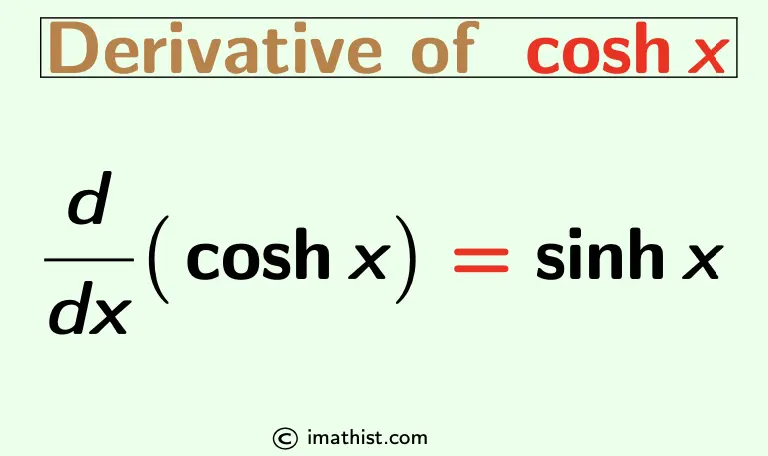
To find the differentiation of coshx, we will use following formulas:

1. sinh x = (e^x – e^-x)/2
2. cosh x = (e^x + e^-x)/2
3. $\dfrac{d}{dx}$(e^mx) = me^mx.

Let us now differentiate coshx.

How to Find the Derivative of coshx

Recall from above that

$\cosh x=\dfrac{e^x+e^{-x}}{2}$.

Differentiating both sides we will get the derivative of coshx.

Therefore,

$\dfrac{d}{dx}\left(\cosh x \right )$ $=\dfrac{d}{dx}\left(\dfrac{e^x+e^{-x}}{2}\right)$

= $\dfrac{1}{2}\Big[ \dfrac{d}{dx}\left(e^x \right) + \dfrac{d}{dx}\left(e^{-x}\right) \Big]$ by the linearity property of derivatives.

= $\dfrac{1}{2}$ ⋅ [e^x + (-e^-x)], by the above Formula (3).

= (e^x – e^-x)/2

= sinhx, by the above Formula (1).

So the derivative of coshx is equal to sinhx.

Have You Read These Derivative?

Derivative of sinh(x)	Derivative of tanx
Derivative of tanh(x)	Derivative of tan 2x

FAQs