Find the Derivative of ln(1/x)

The derivative of ln(1/x) is equal to -1/x, where ln denotes the logarithm with base e, that is, ln(x)=log_ex. In this post, we will find the derivative of ln(1/x).

Note that ln(1/x) is the natural logarithm of 1/x. Its derivative formula is given below:

$\dfrac{d}{dx}\big( \ln (\dfrac{1}{x}) \big)=-\dfrac{1}{x}$.

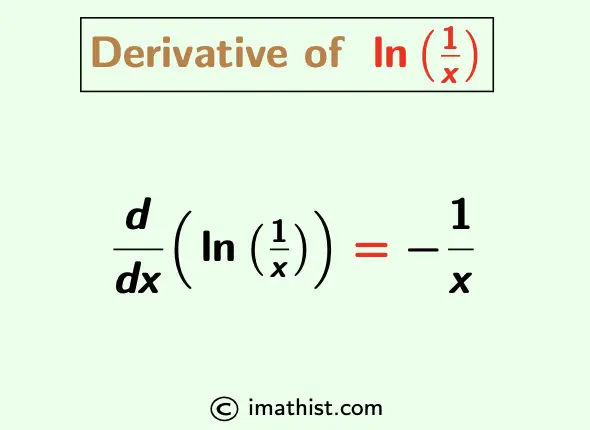
Derivative of ln(1/x) by Chain Rule

Let z=1/x.

So dz/dx = d/dx(x^-1) = -1/x², by the power rule of derivatives.

Now, we have:

$\dfrac{d}{dx} \big( \ln (\dfrac{1}{x}) \big)$

= $\dfrac{d}{dz} \big( \ln z \big) \times \dfrac{dz}{dx}$ by the chain rule of derivative.

= $\dfrac{1}{z} \times \dfrac{-1}{x^2}$ as the derivative of lnx is 1/x and dz/dx= -1/x².

= $\dfrac{1}{1/x} \times \dfrac{-1}{x^2}$ as z=1/x.

= $-x \times \dfrac{1}{x^2}$

= $-\dfrac{1}{x}$

So the derivative of ln(1/x) is equal to -1/x, and this is obtained by the chain rule of derivatives.

More Derivative Problems:

Derivative of $\frac{1}{\ln x}$

Derivative of 1/x

Derivative of sinx/x

FAQs