Find Derivative of root 1-x^2

The derivative of root 1-x^2 is equal to -x/√(1-x²). Here we differentiate square root of 1-x² by chain rule and implicit differentiation method.

Note that

$\dfrac{d}{dx} \Big( \sqrt{1-x^2}\Big)=-\dfrac{x}{\sqrt{1-x^2}}$.

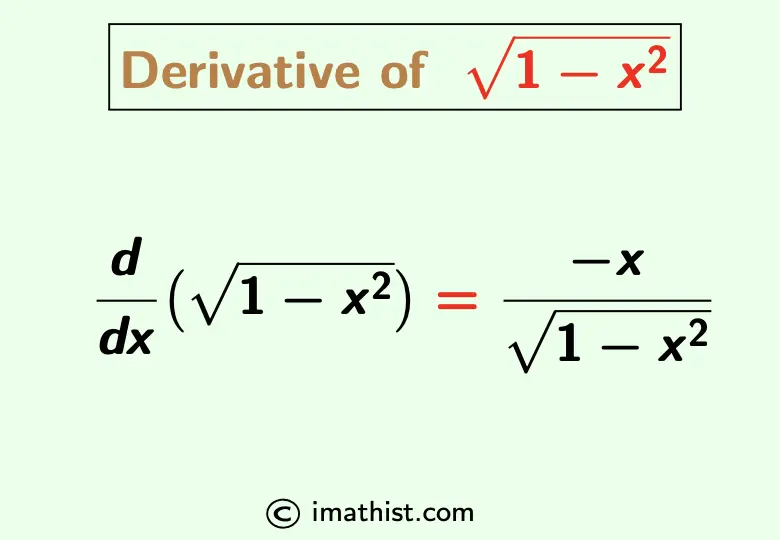
Let us now differentiate root 1-x².

Derivative of root 1-x² by Chain Rule

Question: Find the derivative of square root 1-x².

Answer:

Let us put z = $1-x^2$.

So that $\dfrac{dz}{dx}=-2x$.

By the chain rule, the derivative of root 1-x² is equal to

$\dfrac{d}{dx} \Big( \sqrt{1-x^2}\Big)= \dfrac{d}{dx} ( \sqrt{z})$

= $\dfrac{d}{dz} ( \sqrt{z}) \times \dfrac{dz}{dx}$

= $\dfrac{d}{dz}$ (z^1/2) × (-2x) as dz/dx= -2x.

= $-2x \times \dfrac{1}{2} z^{1/2 -1}$

= $-\dfrac{x}{z^{1/2 }}$

= $-\dfrac{x}{\sqrt{1-x^2}}$ as z=1-x².

So the derivative of square root 1-x² by the chain rule is equal to -x/√(1-x²).

Derivative of root 1-x² by Implicit Differentiation

Answer: The differentiation of square root of 1-x² is equal to -x/√(1-x²).

Explanation:

We will use the implicit differentiation method to find the derivative of square root of 1-x square. So let us put

y = $\sqrt{1-x^2}$.

Squaring both sides, we get that

y² = 1-x².

Differentiating both sides w.r.t x, we get that

$2y \dfrac{dy}{dx}=-2x$

⇒ $\dfrac{dy}{dx}=-\dfrac{x}{y}$

⇒ $\dfrac{dy}{dx}=-\dfrac{x}{\sqrt{1-x^2}}$, putting the value of y.

So the derivative of square root of 1-x^2 is equal to -x/√(1-x²), and this is obtained by the implicit differentiation method.

Also Read: Derivative of root x

Derivative of $\sqrt{\sin x}$

Derivative of $\sqrt{\cos x}$

Derivative of $\sqrt{\tan x}$

Derivative of $\sqrt{\sec x}$

Derivative of $\sqrt{\cot x}$

FAQs