The derivative of root tanx is equal to -cosec2x/(2√cotx). Here we will differentiate square root of cot x by chain rule and also using the first principle of derivatives.
The derivative formula of root cotx is given by
$\dfrac{d}{dx}(\sqrt{\cot x})=-\dfrac{\text{cosec}^2 x}{2\sqrt{\cot x}}$.
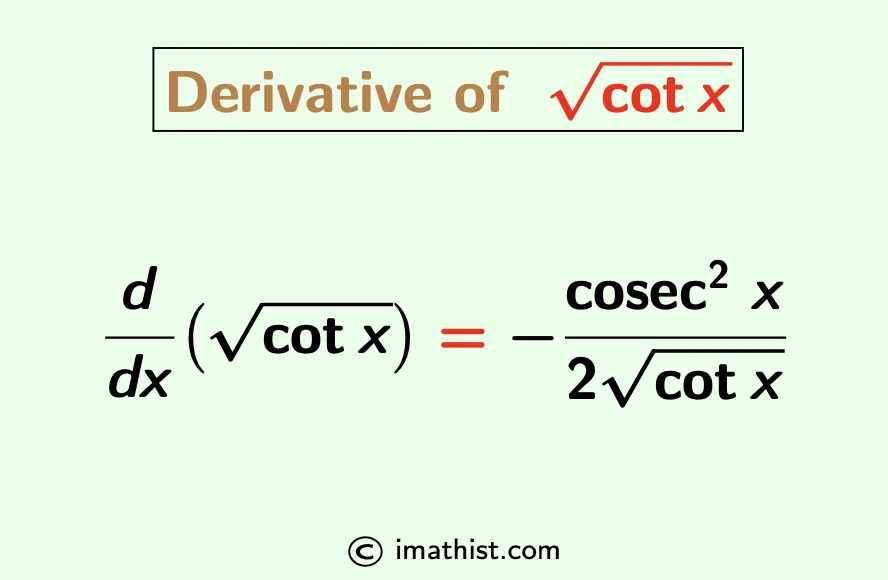
Derivative of square root of cotx from first principle
Question: Find the derivative of $\sqrt{\cot x}$ from first principle.
Solution:
We will follow the below steps to find the derivative of square root of cot x using first principle. The steps are as follows.
Step 1:
Recall, the derivative of a function f(x) by first principle. It is given by the limit below:
$\dfrac{d}{dx}(f(x))$ = limh→0 $\dfrac{f(x+h)-f(x)}{h}$.
Step 2:
Put f(x)=$\sqrt{\cot x}$.
So the derivative of square root cotx will be equal to
$\dfrac{d}{dx}(\sqrt{\cot x})$ = limh→0 $\dfrac{\sqrt{\cot (x+h)}-\sqrt{\cot x}}{h}$
Multiply both the numerator and the denominator by √cot(x + h) + √cotx. This will give us
$\dfrac{d}{dx}(\sqrt{\cot x})$ = limh→0 $\Big[ \dfrac{\sqrt{\cot (x+h)}-\sqrt{\cot x}}{h}$ $\times \dfrac{\sqrt{\cot (x+h)}+\sqrt{\cot x}}{\sqrt{\cot (x+h)}+\sqrt{\cot x}} \Big]$
= limh→0 $\dfrac{(\sqrt{\cot (x+h)})^2-(\sqrt{\cot x})^2}{h(\sqrt{\cot (x+h)}+\sqrt{\cot x})}$, using the algebraic identity (a-b)(a+b)=a2-b2.
= limh→0 $\Big[ \dfrac{\cot (x+h)-\cot x}{h}$ × $\dfrac{1}{\sqrt{\cot (x+h)}+\sqrt{\cot x}} \Big]$ …(∗)
Step 3:
Note that the limit $\lim\limits_{h \to 0} \dfrac{\cot (x+h)-\cot x}{h}$ is equal to $\dfrac{d}{dx}(\cot x)$, by the first principle of derivatives, which is equal to -cosec2x.
Now, from (∗) we deduce (applying product rule) that
$\dfrac{d}{dx}(\sqrt{\cot x})$ = limh→0 $\dfrac{\cot (x+h)-\cot x}{h}$ × limh→0 $\dfrac{1}{\sqrt{\cot (x+h)}+\sqrt{\cot x}}$
= -cosec2x $\times \dfrac{1}{\sqrt{\cot (x+0)}+\sqrt{\cot x}}$
= -cosec2x $ \times \dfrac{1}{2\sqrt{\cot x}}$
= $-\dfrac{\text{cosec}^2 x}{2\sqrt{\cot x}}$
Thus, the derivative of square root of cotx by the first principle is equal to -cosec2x/(2√cotx).
Related Topics:
Derivative of $\sqrt{\sin x}$ from first principle
Derivative of $\sqrt{\cos x}$ from first principle
Derivative of $\sqrt{\cos x}$ by chain rule
Derivative of $\sqrt{\sec x}$ by chain rule
Derivative of root cotx by chain rule
Let u=cotx.
So du/dx = -cosec2x.
Now, by the chain rule, the derivative of square root of cotx is equal to
$\dfrac{d}{dx}(\sqrt{\cot x})$ = $\dfrac{d}{dx}(\sqrt{u})$
= $\dfrac{d}{du}(\sqrt{u}) \times \dfrac{du}{dx}$
= $\dfrac{d}{du}$(u1/2) × -cosec2x
= 1/2 u1/2-1 × -cosec2x
= 1/(2√u) × -cosec2x
= – cosec2x/(2√cotx).
So the derivative of square root of cotx by the chain rule is equal to -cosec2x/(2√cotx).
More Reading: Derivative of $\sqrt{\sin x}$ by chain rule
FAQs
Q1: What is the derivative of root cotx?
Answer: The derivative of square root cotx is equal to -cosec2x/(2√cotx).