The cos^3x formula is given by cos3x = (cos3x + 3cosx)/4. In this post, we learn how to prove the cos cube x formula.
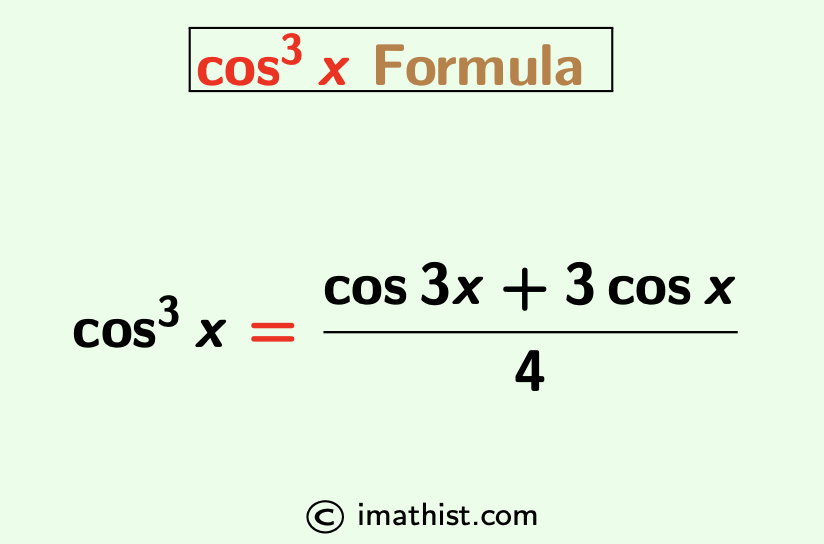
What is cos cube x formula
| Answer: cos3x=(cos3x + 3cosx)/4 is the formula of cos cube x. |
Proof:
We will follow the below steps in order to prove cos cube x formula.
Step 1: First, we use cos3x formula and the formula is given below:
cos3x = 4cos3x – 3cos x.
Step 2: Now we add 3cosx to both sides of the above equation. By doing so, we obtain that
cos3x + 3cox= 4cos3x – 3cos x +3cosx.
⇒ cos3x + 3cox = 4cos3x …(I)
Step 3: Dividing both sides of (I) by 4, we have that
(cos3x + 3cosx)/4 = cos3x.
Therefore, the cos3x formula is obtained as follows: cos3x = (cos3x + 3cosx)/4.
Remark:
Replacing x in the above formula by θ, the formula of cos3θ (cos cube theta) is given by cos3θ = (cos3θ + 3cosθ)/4.
Have You Read These?
| Sin3x Formula | Cos3x Formula |
| sin3x Formula | sinx siny Identity |
| tan(x-y) Formula | cot(x+y) Formula |
| Simplify sin(cos-1x) | cos2x-sin2x Formula |
FAQs
Q1: What is the cos^3x formula?
Answer: The cos^3x formula states that cos3x =(cos3x + 3cosx)/4.
Q2: What is the cos^3θ formula?
Answer: The cos cube theta formula is given by cos3θ = (cos3θ + 3cosθ)/4.