The integration of 1/x is equal to ln|x|+C where ln denotes the natural logarithm, that is, ln|x|=loge|x| and C is the integration constant. In this post, we will learn how to integrate 1/x.
Integration of 1/x Formula
The formula for the integration of 1/x (1 divided by x) is given below.
∫ 1/x dx = ln|x| +C where ln x =logex.
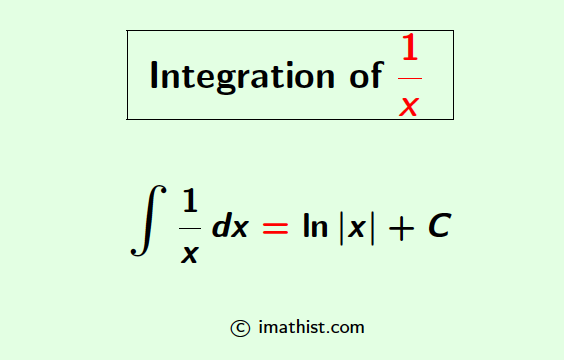
How to Integrate 1/x
Now, we will prove that ∫ 1/x dx = ln|x| +C. Note that 1/x=x-1 cannot be integrated using the power rule integration ∫xn dx = xn+1/(n+1) +C as we have -1+1=0 in the denominator. Thus, to find the integration of 1/x, we will proceed as follows:
Let z=ln x
Differentiating both sides, dz= dx/x. Therefore, we obtain that
∫1/x dx = ∫dx/x = ∫dz
= z+C
= ln x +C
= ln|x|+C as ln is not defined for negative values.
So the integration of 1/x is ln|x|+C where C is the indefinite integral constant.
ALSO READ
Video Solution on Integration of 1/x:
Definite Integral of 1/x
Question: Find the definite integral of 1/x from 1 to 2, that is find ∫12 1/x dx.
Answer:
As the integral of 1/x is equal to lnx, we obtain that
∫12 1/x dx = [ln x]12
⇒ ∫12 1/x dx = ln 2 – ln 1
⇒ ∫12 1/x dx = ln 2 – 0 as the value of ln1 is 0.
⇒ ∫12 1/x dx = ln 2.
So the value of the definite integral of 1/x from 1 to 2 is equal to ln2.
FAQs on Integration of 1/x
Q1: What is the integration of 1/x?
Answer: The integration of 1/x is ln|x|+C.