Find Solution of the Differential Equation dy/dx=x+y

The exact solution of dy/dx=x+y is equal to |x+y+1| = Ce^x where C is a constant. In this post, we will learn how to solve the differential equation dy/dx =x+y.

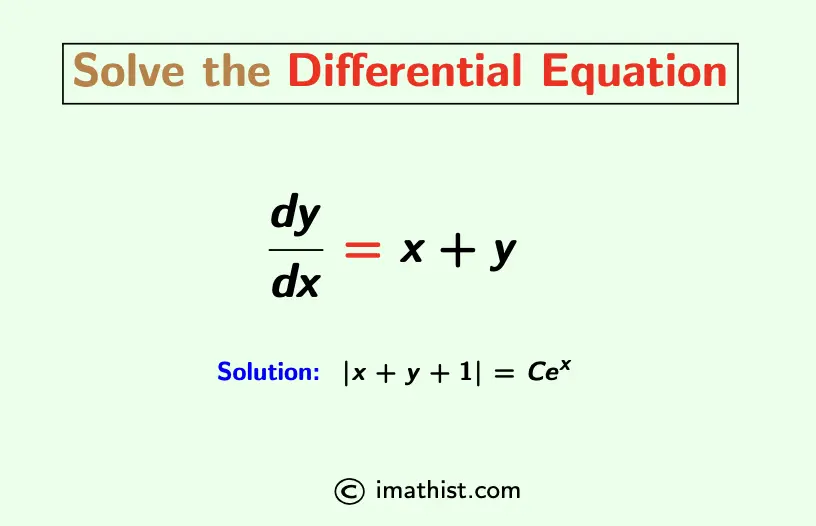
Solve dy/dx=x+y

Question: Find the general solution of $\dfrac{dy}{dx}=x+y$.

Solution:

To solve the given differential equation, we will use the substitute method. Let us put

z=x+y.

Differentiating with respect to x,

$\dfrac{dz}{dx}=1+\dfrac{dy}{dx}$.

⇒ $\dfrac{dy}{dx}=\dfrac{dz}{dx}-1$.

So from the given equation, we obtain that

$\dfrac{dz}{dx}-1=z$

⇒ $\dfrac{dz}{dx}=1+z$

⇒ $\dfrac{dz}{1+z}=dx$

Integrating, $\int \dfrac{dz}{1+z}=\int dx $ +k

⇒ $\ln |1+z|=x+k$

⇒ $\ln |1+x+y|=x+k$ as z=x+y.

⇒ $|1+x+y|=Ce^x$ where C=e^k.

So the general solution of dy/dx=x+y equals to |x+y+1| = Ce^x where C denotes an integral constant.

More Differential Equations:

Solve dy/dx = sin(x+y)

Solve dy/dx = cos(x+y)

FAQs