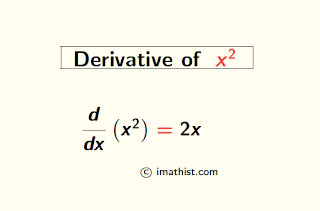Derivative of x^2: Proof by First Principle, Power Rule

The derivative of x² (x square) by first principle is 2x. The function x² denotes the square of x. In this post, we will find the derivative of x square.

The derivative of x square is denoted by d/dx (x²), and its formula is given below:

$\dfrac{d}{dx}$ (x²) = 2x.

Derivative of x² by First Principle

Recall the first principle of derivatives: The derivative of a function f(x) by first principle is given as follows.

$\dfrac{d}{dx}(f(x))$ = lim_h→0 $\dfrac{f(x+h)-f(x)}{h}$

Let f(x)=x²

So the derivative of x square by the first principle is equal to

$\dfrac{d}{dx}(x^2)$ $=\lim\limits_{h \to 0} \dfrac{(x+h)^2-x^2}{h}$

= lim_h→0 $\dfrac{x^2+2xh+h^2-x^2}{h}$ using the algebraic identity (a+b)² = a²+2ab+b².

= lim_h→0 $\dfrac{2xh+h^2}{h}$

= lim_h→0 $\dfrac{h(2x+h)}{h}$

= lim_h→0 $[2x+h]$

= 2x+0

= 2x.

Hence, the derivative of x² by first principle is 2x.

More Derivatives: Derivative of x⁵ by First Principle

Derivative of e^sinx by First Principle

Derivative of x⁶ by First Principle

Derivative of x² by Power Rule

Let us use the power rule of derivatives to find the derivative of x square. The power rule says that the derivative of xⁿ is given by $\dfrac{d}{dx}(x^n)$=nx^n-1.

Putting n=2 in the above rule, we will get the derivative of x².  Thus, we have that

$\dfrac{d}{dx}(x^2)$ =2x^2-1 = 2x¹ =2x.

Hence, the derivative of x² (x square) by the power rule of derivatives is 2x.

More Reading: Derivative of xⁿ

Derivative of 2^x | Derivative of x¹⁰

Question-Answer

Question 1: Find the derivative of $(\ln x)^2$

Solution:

Let z=ln x.

So we have $\dfrac{dz}{dx}=\dfrac{1}{x}$.

Then by the chain rule of derivatives, the derivative of \lnx square is equal to

$\dfrac{d}{dx}(z^2)$ $=\dfrac{d}{dz}(z^2) \cdot \dfrac{dz}{dx}$

$=2z \cdot \dfrac{1}{x}$

$=\dfrac{2}{x} \ln x$ as z=ln x.

Thus, the derivative of (ln x)² is equal to (2/x) ln x.

Also Read: 

Derivative of 1/root(x)

Derivative of root x + 1 by root x

Derivative of 1/x²

Derivative of 1/(1+x²)

FAQs