Derivative of xe^-x by First Principle & Product Rule

The derivative of xe^-x is equal to (1-x)e^-x. In this post, we will find the derivative of xe^-x by the product rule and the first principle of derivatives.

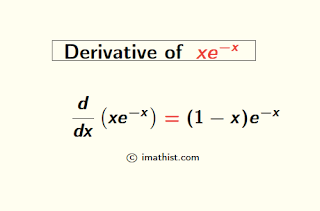
Derivative of xe^-x by First Principle

The derivative of $f(x)=xe^{-x}$by the first principle is given by

$(xe^{-x})’$ = lim_h→0 $\dfrac{(x+h)e^{-(x+h)}-xe^{-x}}{h}$

= lim_h→0 $\dfrac{xe^{-(x+h)}+he^{-(x+h)}-xe^{-x}}{h}$

= lim_h→0 $\big(\dfrac{xe^{-(x+h)}-xe^{-x}}{h}$ $+\dfrac{he^{-(x+h)}}{h} \big)$

= lim_h→0 $\dfrac{xe^{-x}e^{-h}-xe^{-x}}{h}$ + lim_h→0 $e^{-(x+h)}$

= xe^-x lim_h→0 $\dfrac{e^{-h}-1}{h}$ $+e^{-(x+0)}$

= xe^-x lim_h→0 $\dfrac{e^{-h}-1}{-h} \times (-1)$ +e^-x

Let z=-h. Then z →0 as h →0.

= -xe^-x lim_h→0 $\dfrac{e^{z}-1}{z}$ $+e^{-x}$

= -xe^-x ⋅ 1 +e^-x  as we know that the limit of (e^z-1)/z tends to 1 when z tends to 0.

= -xe^-x +e^-x = (1-x)e^-x.

Hence, the derivative of xe^-x from the first principle is equal to (1-x)e^-x.

Derivative of xe^-x by Product Rule

Product rule of derivatives says that if f(x) = g(x) h(x) is a product of two functions, then the derivative of f(x) is given by

$\dfrac{d}{dx}(f(x))$ $=g(x) \dfrac{d}{dx}(h(x))+h(x) \dfrac{d}{dx}(g(x))$

We have f(x)=xe^-x.

Take g(x)=x and h(x)=e^-x in the product rule.

Thus, the derivative of f(x)=xe^-x by the product rule is equal to

 $\dfrac{d}{dx}(xe^{-x})$ $=x \dfrac{d}{dx}(e^{-x})+e^{-x} \dfrac{d}{dx}(x)$

= – xe^-x +e^-x ⋅ 1

= (1-x)e^-x

Hence, the derivative of xe^-x by the product rule is (1-x)e^-x.

Also Read: 

Derivative of 1/root(x) 

Derivative of root x + 1 by root x

Derivative of 1/x² 

Derivative of 1/(1+x²)

FAQs