Derivative of ln(x+1): Proof by First Principle, Chain Rule

The derivative of ln(x+1) is equal to 1/(x+1). Ln(x+1) denotes the natural logarithm of x+1, that is, ln(x+1) = log_e(x+1). Here we will find the derivative of ln(x+1) using the following methods:

1. Chain rule
2. First principle.

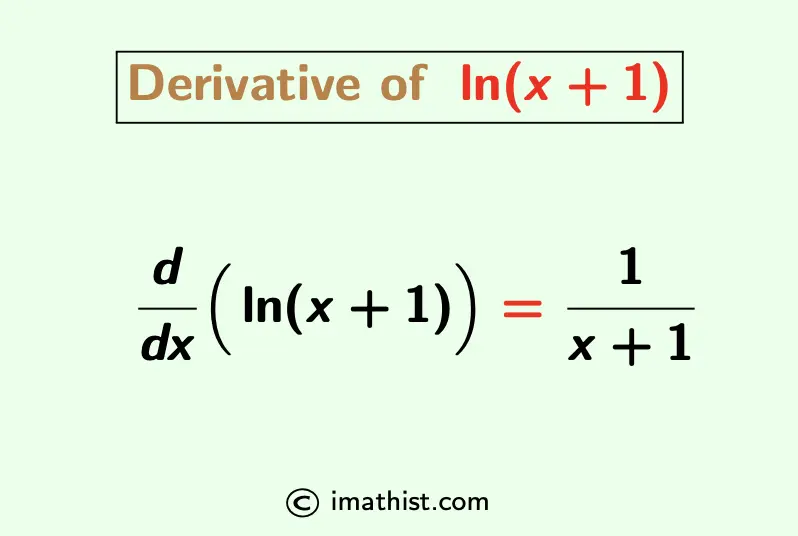
The derivative of ln(x+1) is denoted by d/dx {ln(x+1)} and its formula is given by

$\dfrac{d}{dx} \Big(\ln (x+1) \Big)=\dfrac{1}{x+1}.$

Derivative of ln(x+1) by Chain Rule

Let z=x+1.

So $\dfrac{dz}{dx}$ = 1.

Now by the chain rule of differentiation, the derivative of ln(x+1) will be

$\dfrac{d}{dx} \Big(\ln (x+1) \Big)$ = $\dfrac{d}{dz} \big(\ln z \big) \times \dfrac{dz}{dx}$

= $\dfrac{1}{z} \times 1$ as the derivative of lnx is 1/x.

= $\dfrac{1}{x+1}$ as z=x+1.

So the derivative of ln(x+1) is equal to 1/(x+1), and it is obtained by the chain rule of differentiation.

More Derivatives:

• Derivative of ln(ln x)
• Derivative of 1/lnx
• Derivative of x^lnx

Derivative of ln(x+1) by First Principle

By first principle, $f'(x)$ = lim_h→0 $\dfrac{f(x+h)-f(x)}{h}$.

Put f(x)= ln(x+1).

So $\dfrac{d}{dx} \Big(\ln (x+1) \Big)$ = lim_h→0 $\dfrac{\ln(x+1+h)-\ln (x+1)}{h}$

= lim_h→0 $\dfrac{\ln \Big(\dfrac{x+1+h}{x+1} \Big)}{h}$

= lim_h→0 $\dfrac{\ln \Big(1+\dfrac{h}{x+1} \Big)}{h}$

Let $\dfrac{h}{x+1}$ = z, so that z→0 when h→0. Also, h=z(x+1).

= lim_z→0 $\dfrac{\ln \big(1+z \big)}{z(x+1)}$

= $\dfrac{1}{x+1}$ lim_z→0 $\dfrac{\ln \big(1+z \big)}{z}$

= $\dfrac{1}{x+1} \times 1$, as the limit of ln(1+x)/x is 1 when x→0.

= $\dfrac{1}{x+1}$.

So the derivative of ln(x+1) by the first principle is equal to 1/(x+1).

You Can Read: Derivative of lnu | Log u Derivative

FAQs