Derivative of cosx/x (cosx divided by x)

The derivative of cosx/x (cosx divided by x) is equal to -(xsinx +cosx)/x². Here we will learn to differentiate cosx/x by the quotient rule as well as implicit differentiation method.

Let us now differentiate cosx/x.

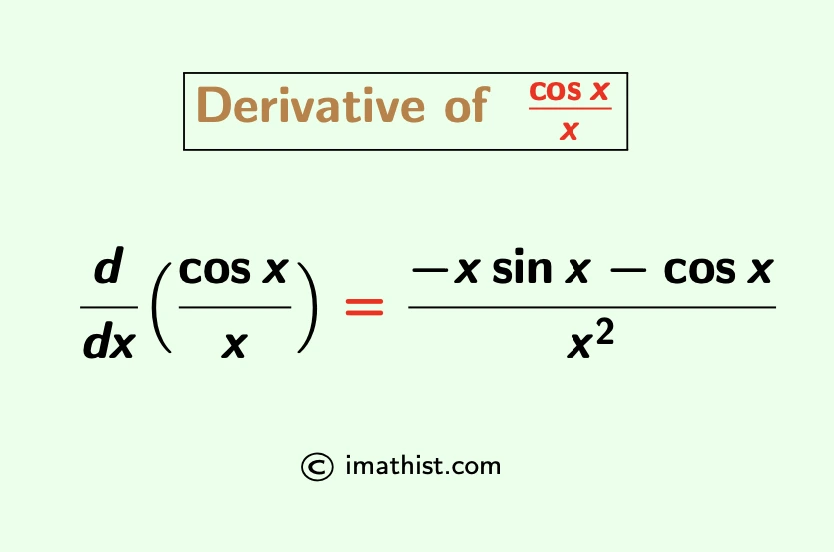
Derivative of cosx/x by Quotient Rule

By the quotient rule, the derivative of $\dfrac{f}{g}$ is given by

$\dfrac{d}{dx}\big( \dfrac{f}{g}\big)=\dfrac{gf’ -fg’}{g^2}$

where ‘ denotes the first order derivative with respect to x.

Put f=cosx and g=x.

So by quotient rule, the derivative of cosx/x will be equal to

$\dfrac{d}{dx}\big( \dfrac{\cos x}{x}\big)=\dfrac{x (\cos x)’ -\cos x(x)’}{x^2}$

= $\dfrac{x (-\sin x) -\cos x \cdot 1}{x^2}$ as the derivative of cosx is -sinx and the derivative of x is 1.

= $\dfrac{-x \sin x -\cos x}{x^2}$.

So the derivative of cosx/x is equal to (-xsinx -cosx)/x² and this is obtained by the quotient rule of derivatives.

Also Read: Derivative of sinx/x

Derivative of x^tanx

Derivative of cosx/x by Implicit Differentiation Method

Let us put

y = $\dfrac{\cos x}{x}$

⇒ xy = cosx.

Differentiating with respect to x, we get that

y + x $\dfrac{dy}{dx} = -\sin x$

⇒ $\dfrac{dy}{dx} =\dfrac{-\sin x -y}{x}$

⇒ $\dfrac{dy}{dx} =\dfrac{-\sin x -\dfrac{\cos x}{x}}{x}$, putting the value of y=cosx/x.

⇒ $\dfrac{dy}{dx} =\dfrac{-x \sin x -\cos x}{x^2}$.

So the derivative of cosx/x is -(xsinx +cosx)/x² and this is proved by the implicit differentiation method.

More Derivatives: Derivative of $\sqrt{\tan x}$

What is the derivative of 2^x

FAQs