Cot2x Identity, Formula, Proof

The cot2x identity is given by cot2x = (cot²x-1)/2cotx. Note that cot2x is the cotangent of the angle 2x. The cot2x formula is as follows:

cot2x = $\dfrac{\cot^2 x -1}{2 \cot x}$.

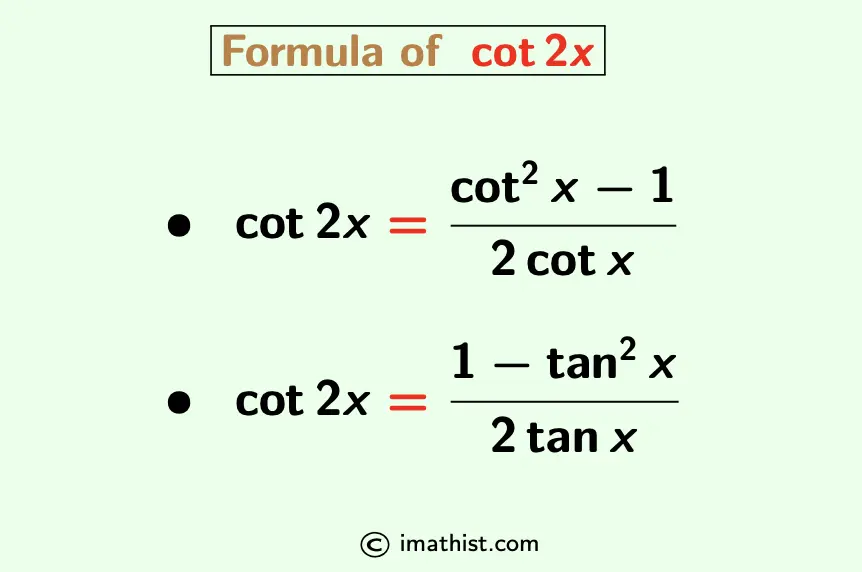
Let us now learn how to prove the cot2x identity.

Cot2x Formula in Terms of cotx

The cot2x formula in terms of cotx is given as follows.

$\boxed{\cot 2x = \dfrac{\cot^2 x -1}{2 \cot x}}$.

Proof:

cot2x = cot(x+x)

= $\dfrac{\cot x \cot x -1}{\cot x +\cot x}$ using the formula cot(a+b) = (cot a cot b -1)/(cot a + cot b)

= $\dfrac{\cot^2 x -1}{2\cot x}$.

So the cot2x formula in terms of cotx is equal to cot2x = (cot²x-1)/2cotx.

You Can Read: Sec2x Identity, Formula | Cosec2x Identity, Formula

Cot2x Formula in Terms of tanx

The cot2x formula in terms of tanx is given below.

$\boxed{\cot 2x = \dfrac{1-\tan^2 x}{2 \tan x}}$.

Proof:

From the above, we have that

$\cot 2x = \dfrac{\cot^2 x -1}{2 \cot x}$

As cotx=1/tanx, we deduce that

$\cot 2x = \dfrac{\frac{1}{\tan^2 x} -1}{\frac{2}{\tan x}}$

$\Rightarrow \cot 2x = \dfrac{1-\tan^2 x}{2\tan x}$.

So the cot2x formula in terms of tanx is equal to cot2x = (1 – tan²x)/2tanx.

Read Also: Sin3x Formula, Identity | Sin³x Formula

Cos3x Formula, Identity

Tan2x Formula in Terms of tan

Remark:

Note that

• cot2x = $\dfrac{1}{\tan 2x}$
• cot2x in terms of tanx and cotx is given by cot2x = $\dfrac{1}{2}(\cot x -\tan x)$

FAQs