Cosec2x Identity | Cosec2x Formula, Proof

The cosec2x identity is given by cosec2x = (tanx + cotx)/2. That is, the formula of cosec 2x is equal to

cosec 2x = $\dfrac{\tan x + \cot x}{2}$.

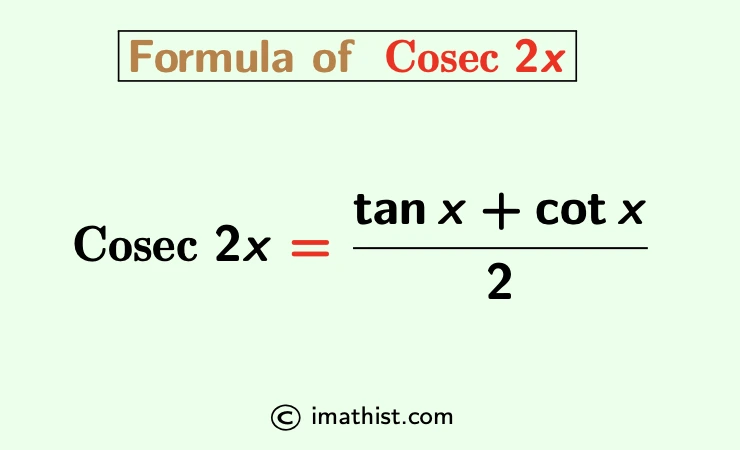
Now, let us learn how to prove the cosec2x formula.

Proof of cosec2x = (tanx+cotx)/2

Note that cosecx is the reciprocal of sinx. So we have that

cosec2x = $\dfrac{1}{\sin 2x}$

= $\dfrac{1}{2\sin x \cos x}$ as we know sin2x= 2sinx cosx.

= $\dfrac{\sin^2 x+\cos^2 x}{2\sin x \cos x}$ using the identity sin²x+cos²x = 1.

= $\dfrac{\sin^2 x}{2\sin x \cos x} + \dfrac{\cos^2 x}{2\sin x \cos x}$

= $\dfrac{\sin x}{2 \cos x} + \dfrac{\cos x}{2\sin x}$

= $\dfrac{\tan x}{2} + \dfrac{\cot x}{2}$

= $\dfrac{\tan x+ \cot x}{2}$

So the formula of cosec2x is equal to cosec2x = (tanx + cotx)/2, and this is the cosec2x identity in terms of tanx and cotx.

You Can Read: sec2x Identity

cos3x Formula | sin3x Formula

Formula of sin(a+b) sin(a-b)

FAQs