The derivative of cos cube x (cos^3x) is equal to -3cos2x sinx. In this post, we will find the derivative of cos cube x using the chain rule.
The derivative formula of cos3x is given as follows:
d/dx (cos3x) = -3cos2x sinx.
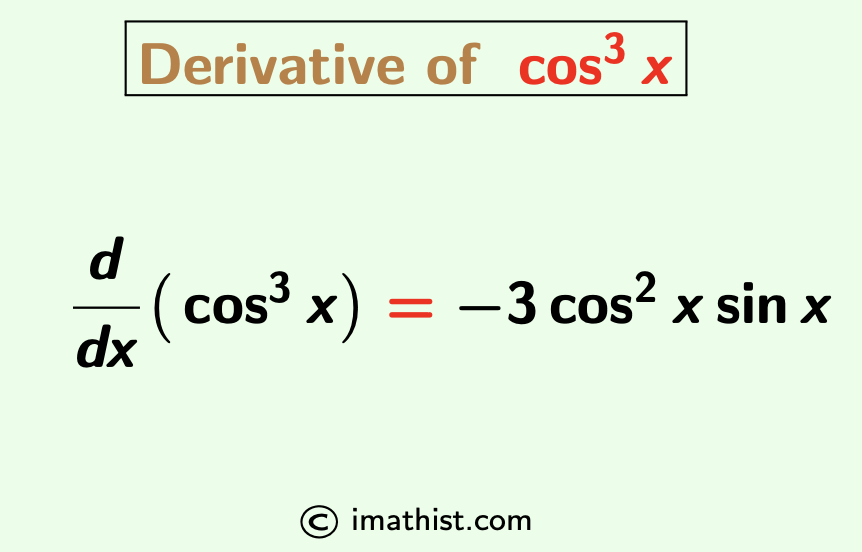
Derivative of Cos^3x
| The derivative of cos3x is -3cos2x sinx. |
Explanation:
As cos3x is a composite function, we will use the chain rule to find its derivative. To do so, let us put
u = cosx.
Thus, cos3x = u3.
As u=cosx, we have that du/dx = -sinx.
Now, by the chain rule the derivative of cos cube x will be equal to
$\dfrac{d}{dx}$ (cos3x) = $\dfrac{d}{dx}$ (u3)
= $\dfrac{d}{du}$ (u3) × $\dfrac{du}{dx}$
= 3u2 × (-sinx) by the power rule of derivatives: d/dx (xn) =nxn-1.
= – 3cos2x sinx.
So the derivative of cos3x (cos cube x) is equal to – 3cos2x sinx, that is, d/dx (cos3x) = -3cos2x sinx which is proved by the chain rule of derivatives.
Have You Read These Derivatives?
| Derivative of cos4x | Derivative of cos(x4) |
| Derivative of sin5x | Derivative of 1/x |
| Derivative of π | Derivative of e1/x |
FAQs
Q1: What is the derivative of cos3x?
Answer: The derivative of cos3x (cos cube x) is – 3cos2x sinx.
Q1: If y=cos3x, then find dy/dx?
Answer: If y=cos3x, then dy/dx = -3cos2x sinx.